IMO Shortlist 2003 problem N4
Dodao/la:
arhiva2. travnja 2012. Let

be an integer greater than
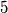
. For each positive integer

, consider the number
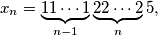
written in base

.
Prove that the following condition holds if and only if
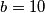
: there exists a positive integer
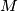
such that for any integer

greater than
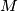
, the number
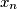
is a perfect square.
%V0
Let $b$ be an integer greater than $5$. For each positive integer $n$, consider the number
$$x_n = \underbrace{11\cdots1}_{n - 1}\underbrace{22\cdots2}_{n}5,$$
written in base $b$.
Prove that the following condition holds if and only if $b = 10$: there exists a positive integer $M$ such that for any integer $n$ greater than $M$, the number $x_n$ is a perfect square.
Izvor: Međunarodna matematička olimpijada, shortlist 2003