IMO Shortlist 2011 problem A4
Dodao/la:
arhiva23. lipnja 2013. Determine all pairs
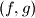
of functions from the set of positive integers to itself that satisfy
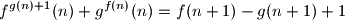
for every positive integer

. Here,
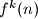
means
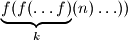
.
Proposed by Bojan Bašić, Serbia
%V0
Determine all pairs $(f,g)$ of functions from the set of positive integers to itself that satisfy
$$f^{g(n)+1}(n) + g^{f(n)}(n) = f(n+1) - g(n+1) + 1$$
for every positive integer $n$. Here, $f^k(n)$ means $\underbrace{f(f(\ldots f)}_{k}(n) \ldots ))$.
Proposed by Bojan Bašić, Serbia
Izvor: Međunarodna matematička olimpijada, shortlist 2011