IMO Shortlist 2013 problem C4
Kvaliteta:
Avg: 0,0Težina:
Avg: 6,5 Let  be a positive integer, and
be a positive integer, and  be a subset of
be a subset of 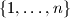 . An
. An  -partition of
-partition of  into
into  parts is a representation of
parts is a representation of  as a sum
as a sum 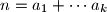 , where the parts
, where the parts 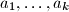 belong to
belong to  and are not necessarily distinct. The number of different parts in such a partition is the number of (distinct) elements in the set
and are not necessarily distinct. The number of different parts in such a partition is the number of (distinct) elements in the set 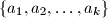 .
.
We say that an A-partition of into
into  parts is optimal if there is no
parts is optimal if there is no  -partition of
-partition of  into
into  parts with
parts with 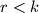 . Prove that any optimal
. Prove that any optimal  -partition of
-partition of  containts at most
containts at most ![\sqrt[3]{6n}](/media/m/f/d/a/fda95afae3f3ebb5dd127b0fe75e439f.png) different parts.
different parts.
 be a positive integer, and
be a positive integer, and  be a subset of
be a subset of 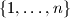 . An
. An  -partition of
-partition of  into
into  parts is a representation of
parts is a representation of  as a sum
as a sum 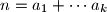 , where the parts
, where the parts 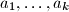 belong to
belong to  and are not necessarily distinct. The number of different parts in such a partition is the number of (distinct) elements in the set
and are not necessarily distinct. The number of different parts in such a partition is the number of (distinct) elements in the set 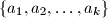 .
.We say that an A-partition of
 into
into  parts is optimal if there is no
parts is optimal if there is no  -partition of
-partition of  into
into  parts with
parts with 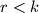 . Prove that any optimal
. Prove that any optimal  -partition of
-partition of  containts at most
containts at most ![\sqrt[3]{6n}](/media/m/f/d/a/fda95afae3f3ebb5dd127b0fe75e439f.png) different parts.
different parts. Izvor: Germany
 Školjka
Školjka 
