IMO 2014 problem 4
Dodao/la:
arhiva21. rujna 2014. Points

and
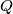
lie on side

of acute-angled triangle

so that
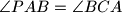
and
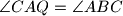
. Points

and

lie on lines
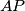
and
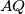
, respectively, such that

is the midpoint of
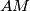
, and
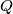
is the midpoint of
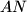
. Prove that lines
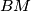
and

intersect on the circumcircle of triangle

.
%V0
Points $P$ and $Q$ lie on side $BC$ of acute-angled triangle $ABC$ so that $\angle PAB = \angle BCA$ and $\angle CAQ = \angle ABC$. Points $M$ and $N$ lie on lines $AP$ and $AQ$, respectively, such that $P$ is the midpoint of $AM$, and $Q$ is the midpoint of $AN$. Prove that lines $BM$ and $CN$ intersect on the circumcircle of triangle $ABC$.
Izvor: International Mathematical Olympiad 2014, day 2