IMO Shortlist 2008 problem C3
Kvaliteta:
Avg: 0,0Težina:
Avg: 7,0 In the coordinate plane consider the set  of all points with integer coordinates. For a positive integer
of all points with integer coordinates. For a positive integer  , two distinct points
, two distinct points  ,
, 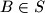 will be called
will be called  -friends if there is a point
-friends if there is a point 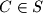 such that the area of the triangle
such that the area of the triangle  is equal to
is equal to  . A set
. A set 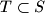 will be called
will be called  -clique if every two points in
-clique if every two points in 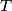 are
are  -friends. Find the least positive integer
-friends. Find the least positive integer  for which there exits a
for which there exits a  -clique with more than 200 elements.
-clique with more than 200 elements.
Proposed by Jorge Tipe, Peru
 of all points with integer coordinates. For a positive integer
of all points with integer coordinates. For a positive integer  , two distinct points
, two distinct points  ,
, 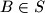 will be called
will be called  -friends if there is a point
-friends if there is a point 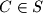 such that the area of the triangle
such that the area of the triangle  is equal to
is equal to  . A set
. A set 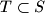 will be called
will be called  -clique if every two points in
-clique if every two points in 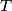 are
are  -friends. Find the least positive integer
-friends. Find the least positive integer  for which there exits a
for which there exits a  -clique with more than 200 elements.
-clique with more than 200 elements. Proposed by Jorge Tipe, Peru
Izvor: Međunarodna matematička olimpijada, shortlist 2008
 Školjka
Školjka 
