Registracija
Što je Školjka?
Školjka je web arhiva zadataka iz matematike, pomoćni alat i sredstvo motivacije namijenjen učenicima i studentima pri pripremi za natjecanja. Sadrži tisuće i tisuće zadataka s raznih matematičkih natjecanja u prethodnih dvadesetak godina te se redovito nadopunjava novim zadacima i natjecanjima.
Why Školjka?
Osim što služi kao baza zadataka, Školjka omogućuje pretraživanje istih po kategorijama i po težini. Učenici tako mogu jednostavno pronaći zadatke točno onog tipa koji ih zanima. Također, Školjka može biti od velike pomoći njihovim mentorima pri organizaciji priprema i predavanja.
Odabrana natjecanja
News
Objavljeni su zadaci s državnih natjecanja za 5., 6. i 7. razred OŠ.
Zadacima možete pristupiti "registracijom" na sljedećim linkovima:
https://www.skoljka.org/archive/os5/
https://www.skoljka.org/archive/os6/
https://www.skoljka.org/archive/os7/
Objavljeni su zadaci s državnih natjecanja iz matematike za 8. razred OŠ.
Napomena: kao što je prije navedeno, eksperimentalno koristimo sučelje za online natjecanja (Marinada i sl.). Kako biste pristupili zadacima, "registrirajte" se preko linka dolje. Ideja je u nekom trenutku napraviti da su zadaci vidljive bez te registracije, ili čak da registracija nije potrebna.
U procesu sam brisanja opskurnih opcija na Školjci i ažuriranja alata na kojima se Školjka bazira (jer je source code zapeo u 2012.), tako da stvari mogu nasumično ne raditi. Pošaljite mi mail ako vam nešto zatreba, a ne radi.
Ivica
Već neko vrijeme se razvija ideja da se Školjka prebaci na novi dizajn koji se koristi za Marinade, druga natjecanja i odnedavno za online tečaj MetaMath.
Stari dizajn je pretrpan razno raznim mogućnostima koje se uglavnom ne koriste i nije pretjerano pregledan. Novi dizajn je pak puno kompaktniji i potencijalno puno pregledniji, čak i za stara natjecanja.
Budući da smo krenuli dodavati osnovnoškolska natjecanja, eksperimentalno ćemo to napraviti na novom "Marinada" sučelju Školjke.
Ideja je sljedeća:
- za svaki razred ćemo napraviti po jedno "natjecanje";
- u to "natjecanje" ćemo dodavati općinska, županijska i državna natjecanja, po jedan lanac zadataka za svaku godinu i razinu natjecanja;
- općinska, županijska i državna će biti odvojena u različite kategorije, kako inače budu algebra, geometrija, kombinatorika, teorija brojeva itd.
Par napomena:
- Nova Školjka nema mogućnost označavanja samome sebi da ste riješili zadatak, no naći ćemo neko privremeno rješenje dok ne poboljšamo sučelje.
- Za razliku od stare Školjke, nova Školjka razlikuje između polaznika/natjecatelja i organizatora. Polaznici (učenici koji se pripremaju za natjecanja) neće moći vidjeti tko je što riješio.
- Očekujemo primjedbe i komentare -- pišite ih u Obavijestima unutar samog natjecanja. Nažalost, nećemo imati centralizirano mjesto za pitanja za sada.
- Ovo je eksperimentalno, vidjet ćemo i mi i vi na što će to ličiti. Konkretno, postoji mogućnost da odustanemo i vratimo sve na običnu Školjku.
Nedavno objavljeni zadaci
Niz znamenaka sastoji se od, redom napisana, prva 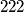 prirodna broja. U tom nizu precrtamo znamenke koje se nalaze na neparnim mjestima. Nakon toga ponovno precrtamo znamenke koje se nalaze na (novim) neparnim mjestima. Taj postupak ponavljamo sve dok ne ostane samo jedna znamenka. Koja će to znamenka biti?
prirodna broja. U tom nizu precrtamo znamenke koje se nalaze na neparnim mjestima. Nakon toga ponovno precrtamo znamenke koje se nalaze na (novim) neparnim mjestima. Taj postupak ponavljamo sve dok ne ostane samo jedna znamenka. Koja će to znamenka biti?
 Školjka
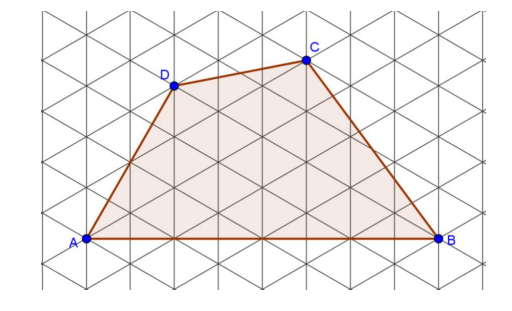
Školjka  m. Izračunaj opseg i površinu četverokuta
m. Izračunaj opseg i površinu četverokuta 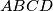 .
.