MEMO 2011 pojedinačno problem 1
Kvaliteta:
Avg: 4,0Težina:
Avg: 6,0 Initially, only the integer 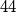 is written on a board. An integer a on the board can be re- placed with four pairwise different integers
is written on a board. An integer a on the board can be re- placed with four pairwise different integers 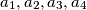 such that the arithmetic mean
such that the arithmetic mean 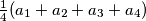 of the four new integers is equal to the number
of the four new integers is equal to the number  . In a step we simultaneously replace all the integers on the board in the above way. After
. In a step we simultaneously replace all the integers on the board in the above way. After 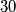 steps we end up with
steps we end up with 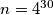 integers
integers 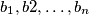 on the board. Prove that
on the board. Prove that 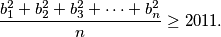
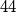 is written on a board. An integer a on the board can be re- placed with four pairwise different integers
is written on a board. An integer a on the board can be re- placed with four pairwise different integers 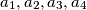 such that the arithmetic mean
such that the arithmetic mean 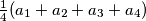 of the four new integers is equal to the number
of the four new integers is equal to the number  . In a step we simultaneously replace all the integers on the board in the above way. After
. In a step we simultaneously replace all the integers on the board in the above way. After 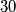 steps we end up with
steps we end up with 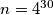 integers
integers 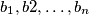 on the board. Prove that
on the board. Prove that 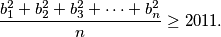
Izvor: Srednjoeuropska matematička olimpijada 2011, pojedinačno natjecanje, problem 1
 Školjka
Školjka 
