IMO Shortlist 2010 problem C2
Kvaliteta:
Avg: 0,0Težina:
Avg: 6,0 On some planet, there are 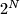 countries
countries 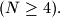 Each country has a flag
Each country has a flag  units wide and one unit high composed of
units wide and one unit high composed of  fields of size
fields of size 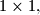 each field being either yellow or blue. No two countries have the same flag. We say that a set of
each field being either yellow or blue. No two countries have the same flag. We say that a set of  flags is diverse if these flags can be arranged into an
flags is diverse if these flags can be arranged into an 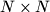 square so that all
square so that all  fields on its main diagonal will have the same color. Determine the smallest positive integer
fields on its main diagonal will have the same color. Determine the smallest positive integer  such that among any
such that among any  distinct flags, there exist
distinct flags, there exist  flags forming a diverse set.
flags forming a diverse set.
Proposed by Tonći Kokan, Croatia
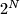 countries
countries 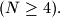 Each country has a flag
Each country has a flag  units wide and one unit high composed of
units wide and one unit high composed of  fields of size
fields of size 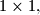 each field being either yellow or blue. No two countries have the same flag. We say that a set of
each field being either yellow or blue. No two countries have the same flag. We say that a set of  flags is diverse if these flags can be arranged into an
flags is diverse if these flags can be arranged into an 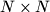 square so that all
square so that all  fields on its main diagonal will have the same color. Determine the smallest positive integer
fields on its main diagonal will have the same color. Determine the smallest positive integer  such that among any
such that among any  distinct flags, there exist
distinct flags, there exist  flags forming a diverse set.
flags forming a diverse set.Proposed by Tonći Kokan, Croatia
Izvor: Međunarodna matematička olimpijada, shortlist 2010
 Školjka
Školjka 
