MEMO 2014 ekipno problem 7
Kvaliteta:
Avg: 1,0Težina:
Avg: 5,0 A finite set of positive integers  is called meanly if for each of its nonempty subsets the arithmetic mean of its elements is also a positive integer. In other words, A is meanly if
is called meanly if for each of its nonempty subsets the arithmetic mean of its elements is also a positive integer. In other words, A is meanly if 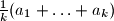 is an integer whenever
is an integer whenever 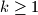 and
and 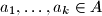 are distinct.
are distinct.
Given a positive integer , determine the least possible sum of the elements of a meanly
, determine the least possible sum of the elements of a meanly  -element set.
-element set.
 is called meanly if for each of its nonempty subsets the arithmetic mean of its elements is also a positive integer. In other words, A is meanly if
is called meanly if for each of its nonempty subsets the arithmetic mean of its elements is also a positive integer. In other words, A is meanly if 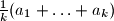 is an integer whenever
is an integer whenever 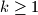 and
and 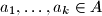 are distinct.
are distinct.Given a positive integer
 , determine the least possible sum of the elements of a meanly
, determine the least possible sum of the elements of a meanly  -element set.
-element set. Izvor: Srednjoeuropska matematička olimpijada 2014, ekipno natjecanje, problem 7
 Školjka
Školjka