Trokutu
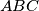
upisana je kružnica polumjera

sa središtem u točki
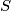
. Pravac kroz točku
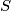
siječe stranice
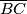
i

redom u točkama
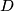
i
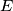
. Dokažite da za površinu

trokuta

vrijedi

. Kada vrijedi jednakost?
%V0
Trokutu $ABC$ upisana je kružnica polumjera $r$ sa središtem u točki $S$. Pravac kroz točku $S$ siječe stranice $\overline{BC}$ i $\overline{CA}$ redom u točkama $D$ i $E$. Dokažite da za površinu $P$ trokuta $CED$ vrijedi $P\geq 2r^2$. Kada vrijedi jednakost?