Neka su
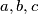
prirodni brojevi takvi da je
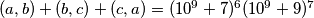
. Neka je
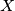
najmanja vrijednost koju može poprimiti
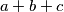
. Odredi zadnjih
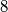
znamenaka od
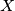
. Brojevi
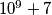
i
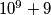
su prosti.
Let
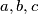
be positive integers such that
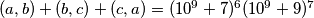
. Let
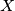
be the least possible value that
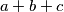
can obtain. Find the last
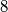
digits of
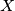
. Note that both
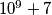
and
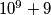
are prime.
[lang=hr]
Neka su $a, b, c$ prirodni brojevi takvi da je $(a,b)+(b,c)+(c,a)=(10^9+7)^6 (10^9+9)^7$. Neka je $X$ najmanja vrijednost koju može poprimiti $a+b+c$. Odredi zadnjih $8$ znamenaka od $X$. Brojevi $10^9+7$ i $10^9+9$ su prosti.
[/lang]
[lang=en]
Let $a, b, c$ be positive integers such that $(a,b)+(b,c)+(c,a)=(10^9+7)^6 (10^9+9)^7$. Let $X$ be the least possible value that $a+b+c$ can obtain. Find the last $8$ digits of $X$. Note that both $10^9+7$ and $10^9+9$ are prime.
[/lang]