Vrlo često je u zadacima iz teorije brojeva potrebno odrediti najveći zajednički djelitelj nekih dvaju cijelih brojeva. S konkretnim brojevima je postupak jasan, odredimo njihov rastav na proste faktore i točno sve ono što im je u presjeku je njihov najveći zajednički djelitelj. Recimo, 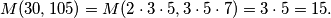 (Podsjetnik: najveći zajednički djelitelj brojeva
(Podsjetnik: najveći zajednički djelitelj brojeva  i
i  najčešće označavamo s
najčešće označavamo s 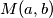 . U stranoj literaturi obično se može vidjeti oznaku
. U stranoj literaturi obično se može vidjeti oznaku 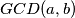 .)
.)
Ipak, u zadacima se češće susrećemo s određivanjem najvećeg zajedničkog djelitelja nekih algebarskih izraza. Primjerice, za relativno proste brojeve  i
i  , vrijedi
, vrijedi 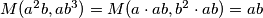 . Naime,
. Naime,  i
i  su relativno prosti pa nemaju zajedničkih djelitelja osim
su relativno prosti pa nemaju zajedničkih djelitelja osim 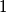 , a onda to vrijedi i za izraze
, a onda to vrijedi i za izraze  i
i 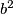 .
.
Međutim, ovakvi argumenti su dosta ograničeni. Primjerice, njima ne možemo reći ništa o 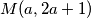 za proizvoljan
za proizvoljan  . Kao jedno od rješenja tog problema, nudi se takozvani Euklidov algoritam, koji kaže da za proizvoljne cijele brojeve
. Kao jedno od rješenja tog problema, nudi se takozvani Euklidov algoritam, koji kaže da za proizvoljne cijele brojeve  i
i  vrijedi
vrijedi 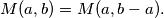
Dokažimo tu tvrdnju. Neka je 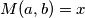 i
i 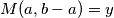 . Tada vrijedi
. Tada vrijedi 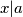 te
te 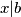 pa je
pa je  i
i 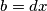 , za neke cijele brojeve
, za neke cijele brojeve 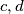 . Tada je
. Tada je 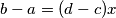 pa
pa 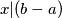 . Znači da je
. Znači da je  zajednički djelitelj brojeva
zajednički djelitelj brojeva  i
i 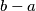 , a s obzirom da je
, a s obzirom da je 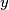 njihov najveći zajednički djelitelj, mora vrijediti
njihov najveći zajednički djelitelj, mora vrijediti 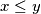 .
.
No, analognu argumentaciju možemo primijeniti i s druge strane. Kako 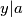 i
i 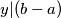 , vrijedi
, vrijedi 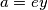 ,
, 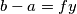 , za neke cijele brojeve
, za neke cijele brojeve 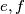 . Tada je
. Tada je 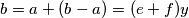 pa
pa 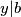 . Dakle,
. Dakle, 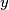 je zajednički djelitelj brojeva
je zajednički djelitelj brojeva  i
i  , a
, a  je po definiciji najveći takav pa mora biti
je po definiciji najveći takav pa mora biti 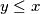 . Zato zaključujemo da je
. Zato zaključujemo da je 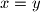 .
.
Kao rješenje upišite najveći zajednički djelitelj brojeva 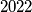 i
i 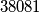 .
.
Vrlo često je u zadacima iz teorije brojeva potrebno odrediti najveći zajednički djelitelj nekih dvaju cijelih brojeva. S konkretnim brojevima je postupak jasan, odredimo njihov rastav na proste faktore i točno sve ono što im je u presjeku je njihov najveći zajednički djelitelj. Recimo,
$$M(30, 105) = M(2 \cdot 3 \cdot 5, 3 \cdot 5 \cdot 7) = 3 \cdot 5 = 15.$$
(\textit{Podsjetnik: najveći zajednički djelitelj brojeva } $a$ \textit{ i } $b$ \textit{ najčešće označavamo s } $M(a,b)$. \textit{U stranoj literaturi obično se može vidjeti oznaku } $GCD(a,b)$.)
Ipak, u zadacima se češće susrećemo s određivanjem najvećeg zajedničkog djelitelja nekih algebarskih izraza. Primjerice, za relativno proste brojeve $a$ i $b$, vrijedi $M(a^2b,ab^3) = M(a \cdot ab, b^2 \cdot ab) = ab$. Naime, $a$ i $b$ su relativno prosti pa nemaju zajedničkih djelitelja osim $1$, a onda to vrijedi i za izraze $a$ i $b^2$.
Međutim, ovakvi argumenti su dosta ograničeni. Primjerice, njima ne možemo reći ništa o $M(a,2a+1)$ za proizvoljan $a$. Kao jedno od rješenja tog problema, nudi se takozvani \textbf{Euklidov algoritam}, koji kaže da za proizvoljne cijele brojeve $a$ i $b$ vrijedi
$$M(a,b)=M(a,b-a).$$
Dokažimo tu tvrdnju. Neka je $M(a,b)=x$ i $M(a,b-a)=y$. Tada vrijedi $x | a$ te $x | b$ pa je $a=cx$ i $b=dx$, za neke cijele brojeve $c,d$. Tada je $b-a=(d-c)x$ pa $x | (b-a)$.
Znači da je $x$ zajednički djelitelj brojeva $a$ i $b-a$, a s obzirom da je $y$ njihov najveći zajednički djelitelj, mora vrijediti $x \leq y$.
No, analognu argumentaciju možemo primijeniti i s druge strane. Kako $y | a$ i $y | (b - a)$, vrijedi $a=ey$, $b-a=fy$, za neke cijele brojeve $e,f$. Tada je $b=a+(b-a)=(e+f)y$ pa $y | b$. Dakle, $y$ je zajednički djelitelj brojeva $a$ i $b$, a $x$ je po definiciji najveći takav pa mora biti $y \leq x$. Zato zaključujemo da je $x=y$.
Kao rješenje upišite najveći zajednički djelitelj brojeva $2022$ i $38081$.
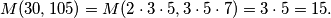 (Podsjetnik: najveći zajednički djelitelj brojeva
(Podsjetnik: najveći zajednički djelitelj brojeva  i
i  najčešće označavamo s
najčešće označavamo s 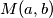 . U stranoj literaturi obično se može vidjeti oznaku
. U stranoj literaturi obično se može vidjeti oznaku 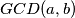 .)
.) i
i  , vrijedi
, vrijedi 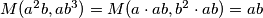 . Naime,
. Naime,  i
i  su relativno prosti pa nemaju zajedničkih djelitelja osim
su relativno prosti pa nemaju zajedničkih djelitelja osim 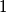 , a onda to vrijedi i za izraze
, a onda to vrijedi i za izraze  i
i 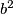 .
.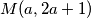 za proizvoljan
za proizvoljan  . Kao jedno od rješenja tog problema, nudi se takozvani Euklidov algoritam, koji kaže da za proizvoljne cijele brojeve
. Kao jedno od rješenja tog problema, nudi se takozvani Euklidov algoritam, koji kaže da za proizvoljne cijele brojeve  i
i  vrijedi
vrijedi 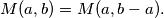
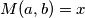 i
i 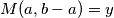 . Tada vrijedi
. Tada vrijedi 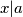 te
te 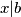 pa je
pa je  i
i 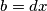 , za neke cijele brojeve
, za neke cijele brojeve 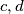 . Tada je
. Tada je 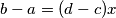 pa
pa 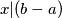 . Znači da je
. Znači da je  zajednički djelitelj brojeva
zajednički djelitelj brojeva  i
i 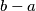 , a s obzirom da je
, a s obzirom da je 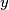 njihov najveći zajednički djelitelj, mora vrijediti
njihov najveći zajednički djelitelj, mora vrijediti 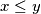 .
.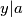 i
i 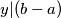 , vrijedi
, vrijedi 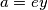 ,
, 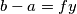 , za neke cijele brojeve
, za neke cijele brojeve 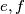 . Tada je
. Tada je 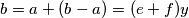 pa
pa 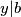 . Dakle,
. Dakle, 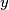 je zajednički djelitelj brojeva
je zajednički djelitelj brojeva  i
i  , a
, a  je po definiciji najveći takav pa mora biti
je po definiciji najveći takav pa mora biti 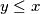 . Zato zaključujemo da je
. Zato zaključujemo da je 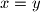 .
.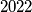 i
i 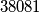 .
. 