Vrijeme: 07:28
Teorija brojeva: Diofantske jednadžbe 2 - RJEŠENJE
Ako je 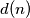 broj djelitelja broja
broj djelitelja broja  , a
, a 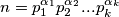 prosta faktorizacija broja
prosta faktorizacija broja  , vrijedi poznata formula
, vrijedi poznata formula 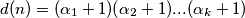 .
.
Ako je 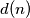 neparan, zaključujemo da je svaki od gore napisanih faktora također neparan pa je
neparan, zaključujemo da je svaki od gore napisanih faktora također neparan pa je 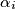 paran za sve
paran za sve 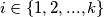 . Zato je
. Zato je  kvadrat prirodnog broja, a tako je i
kvadrat prirodnog broja, a tako je i 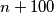 .
.
Imamo 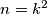 ,
, 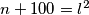 . Slijedi:
. Slijedi:
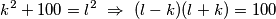
Vrijedi 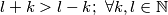 pa imamo mogućnosti:
pa imamo mogućnosti:
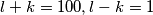
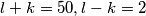
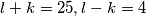
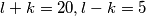
Jedino cjelobrojno rješenje ovdje je 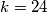 , a može se provjeriti da
, a može se provjeriti da 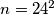 doista zadovoljava uvjete zadatka.
doista zadovoljava uvjete zadatka.
