Točno
24. prosinca 2022. 01:43 (1 godina, 4 mjeseci)
Odredi sva realna rješenja jednadžbe
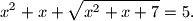
%V0
Odredi sva realna rješenja jednadžbe $$
x^2+x+\sqrt{x^2+x+7}=5.
$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Koristimo substituciju
$$ y = x^2 + x$$
Onda imamo
$$y + \sqrt{y + 7} = 5$$
$$...$$
$$(y - 2)(y - 9) = 0$$
Rješenje $y = 9$ izbacujemo jer je nastao kvadriranjem obe strane.
$$y = 2$$ je jedino rješenje.
$$x^2 + x = 2$$
$$x_1 = 1$$
$$x_2 = -2$$
| 18. rujna 2023. 18:46 | d | Točno |