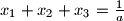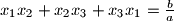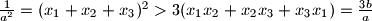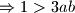Točno
4. prosinca 2013. 19:39 (10 godine, 4 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Ocjene: (1)
Komentari:
11235, 1. rujna 2019. 21:35
grga, 8. siječnja 2014. 16:44
ovo je super.
ja bih mozda samo pripazio na jednu stvar.. mozda je sigurnije ako bi prvo definirali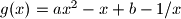 ,
, 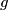 je funkcija cija je domena
je funkcija cija je domena 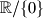 . ta funkcija na svojoj domeni ima prema uvjetu zadatka 3 razlicite nultocke. ako tu funkciju pomnozimo s funkcijom
. ta funkcija na svojoj domeni ima prema uvjetu zadatka 3 razlicite nultocke. ako tu funkciju pomnozimo s funkcijom 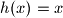 , definiranu takoder na domeni
, definiranu takoder na domeni 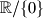 , dobili smo funkciju
, dobili smo funkciju 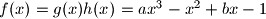 , takoder definiranu na
, takoder definiranu na 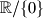 koja ima jednak broj nultocaka kao i
koja ima jednak broj nultocaka kao i 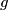 . dakle uvjet zadatka je sad ekvivalentan s tim da funkcija
. dakle uvjet zadatka je sad ekvivalentan s tim da funkcija 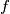 na domeni
na domeni 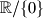 ima 3 razlicite nulotcke. no, buduci da
ima 3 razlicite nulotcke. no, buduci da 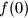 ima smisla, i nije jednak
ima smisla, i nije jednak 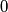 , tj jednak je
, tj jednak je 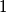 , mozemo
, mozemo 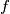 promatrati na siroj domeni,
promatrati na siroj domeni, 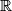 , gdje ima jednak broj razlcitih nultocaka kao na
, gdje ima jednak broj razlcitih nultocaka kao na 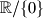 .
.
onako.. naravno da nije bilo potrebno da pises cijelo ovo obrazlozenje, no nisam bio siguran dali znas da je ovo potrebno provjeriti, pa za svaki slucaj.
offtopic: kako napisati R {0}, ako da mi ovaj znak "bez" bude u pravu stranu
ja bih mozda samo pripazio na jednu stvar.. mozda je sigurnije ako bi prvo definirali
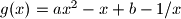 ,
, 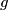 je funkcija cija je domena
je funkcija cija je domena 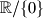 . ta funkcija na svojoj domeni ima prema uvjetu zadatka 3 razlicite nultocke. ako tu funkciju pomnozimo s funkcijom
. ta funkcija na svojoj domeni ima prema uvjetu zadatka 3 razlicite nultocke. ako tu funkciju pomnozimo s funkcijom 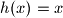 , definiranu takoder na domeni
, definiranu takoder na domeni 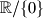 , dobili smo funkciju
, dobili smo funkciju 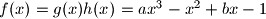 , takoder definiranu na
, takoder definiranu na 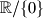 koja ima jednak broj nultocaka kao i
koja ima jednak broj nultocaka kao i 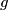 . dakle uvjet zadatka je sad ekvivalentan s tim da funkcija
. dakle uvjet zadatka je sad ekvivalentan s tim da funkcija 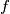 na domeni
na domeni 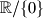 ima 3 razlicite nulotcke. no, buduci da
ima 3 razlicite nulotcke. no, buduci da 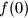 ima smisla, i nije jednak
ima smisla, i nije jednak 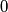 , tj jednak je
, tj jednak je 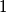 , mozemo
, mozemo 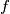 promatrati na siroj domeni,
promatrati na siroj domeni, 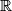 , gdje ima jednak broj razlcitih nultocaka kao na
, gdje ima jednak broj razlcitih nultocaka kao na 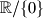 .
.onako.. naravno da nije bilo potrebno da pises cijelo ovo obrazlozenje, no nisam bio siguran dali znas da je ovo potrebno provjeriti, pa za svaki slucaj.
offtopic: kako napisati R {0}, ako da mi ovaj znak "bez" bude u pravu stranu
 Školjka
Školjka  i
i  realni brojevi. Poznato je da parabola
realni brojevi. Poznato je da parabola 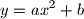 siječe krivulju
siječe krivulju 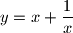 u točno tri točke. Dokaži da vrijedi
u točno tri točke. Dokaži da vrijedi 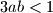 .
. 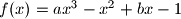
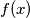 ima 3 razlicite nultocke
ima 3 razlicite nultocke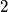 razlicita lokalna ekstrema.
razlicita lokalna ekstrema.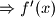 ima 2 realne razlicite nultocke
ima 2 realne razlicite nultocke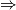 diskriminanta od
diskriminanta od 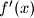 je pozitivna
je pozitivna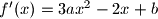
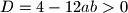
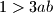
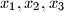 nultocke od
nultocke od