The altitudes through the vertices
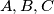
of an acute-angled triangle

meet the opposite sides at
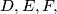
respectively. The line through
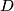
parallel to
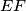
meets the lines
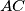
and

at
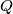
and
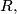
respectively. The line
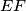
meets

at
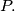
Prove that the circumcircle of the triangle
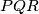
passes through the midpoint of
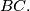
%V0
The altitudes through the vertices $A,B,C$ of an acute-angled triangle $ABC$ meet the opposite sides at $D,E, F,$ respectively. The line through $D$ parallel to $EF$ meets the lines $AC$ and $AB$ at $Q$ and $R,$ respectively. The line $EF$ meets $BC$ at $P.$ Prove that the circumcircle of the triangle $PQR$ passes through the midpoint of $BC.$