Hrvatska matematička olimpijada 1994 - Drugi dan - Zadatak 2
Dodao/la:
mljulj12. travnja 2012. Za svaki prirodan broj

određeni su cijeli brojevi
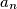
i
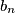
tako da je
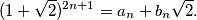
a) Dokažite da su
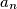
i
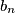
neparni za svaki

.
b) Dokažite da je
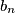
hipotenuza pravokutnog trokuta čije su katete
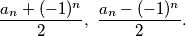
%V0
Za svaki prirodan broj $n$ određeni su cijeli brojevi $a_n$ i $b_n$ tako da je
$$ (1+\sqrt{2})^{2n+1}=a_n+b_n \sqrt{2}.$$
a) Dokažite da su $a_n$ i $b_n$ neparni za svaki $n$.
b) Dokažite da je $b_n$ hipotenuza pravokutnog trokuta čije su katete
$$ \frac{a_n+(-1)^n}{2}, \ \frac{a_n-(-1)^n}{2}. $$
Izvor: Hrvatska matematička olimpijada 1994.