Let

be a point interior to triangle

(with
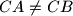
). The lines
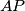
,
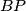
and
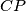
meet again its circumcircle
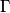
at
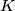
,
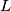
, respectively

. The tangent line at
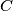
to
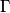
meets the line

at

. Show that from
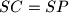
follows
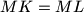
.
Proposed by Marcin E. Kuczma, Poland
%V0
Let $P$ be a point interior to triangle $ABC$ (with $CA \neq CB$). The lines $AP$, $BP$ and $CP$ meet again its circumcircle $\Gamma$ at $K$, $L$, respectively $M$. The tangent line at $C$ to $\Gamma$ meets the line $AB$ at $S$. Show that from $SC = SP$ follows $MK = ML$.
Proposed by Marcin E. Kuczma, Poland