Let  be a triangle with
be a triangle with 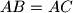 and let
and let 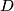 be the midpoint of
be the midpoint of 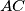 . The angle bisector of
. The angle bisector of 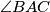 intersects the circle through
intersects the circle through 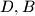 and
and 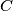 at the point
at the point 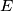 inside the triangle
inside the triangle  . The line
. The line 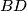 intersects the circle through
intersects the circle through 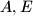 and
and  in two points
in two points  and
and 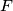 . The lines
. The lines 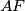 and
and 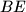 meet at a point
meet at a point  , and the lines
, and the lines 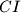 and
and 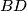 meet at a point
meet at a point 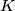 . Show that
. Show that  is the incentre of triangle
is the incentre of triangle 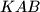 .
.
Proposed by Jan Vonk, Belgium and Hojoo Lee, South Korea
 be a triangle with
be a triangle with 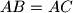 and let
and let 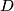 be the midpoint of
be the midpoint of 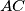 . The angle bisector of
. The angle bisector of 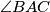 intersects the circle through
intersects the circle through 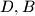 and
and 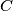 at the point
at the point 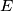 inside the triangle
inside the triangle  . The line
. The line 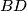 intersects the circle through
intersects the circle through 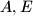 and
and  in two points
in two points  and
and 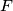 . The lines
. The lines 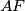 and
and 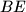 meet at a point
meet at a point  , and the lines
, and the lines 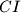 and
and 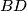 meet at a point
meet at a point 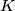 . Show that
. Show that  is the incentre of triangle
is the incentre of triangle 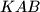 .
.Proposed by Jan Vonk, Belgium and Hojoo Lee, South Korea
 Školjka
Školjka