Funkcije 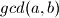 i
i 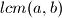 su najcesci zapis za najveceg zajednickog djeljitelja (Greatest Common Divisor) i najmanjeg zajednickog visekratnika (Lowest Common Multiple).
su najcesci zapis za najveceg zajednickog djeljitelja (Greatest Common Divisor) i najmanjeg zajednickog visekratnika (Lowest Common Multiple).
Primjetimo prvo da je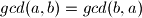 i
i 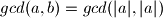 (Jer predznak broja ne mijenja njegove proste djeljitelje)
(Jer predznak broja ne mijenja njegove proste djeljitelje)
Funkciju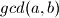 mozemo racunati mnogo brze nego faktorizacijom, pomocu Euklidovog algoritma.
mozemo racunati mnogo brze nego faktorizacijom, pomocu Euklidovog algoritma.
Euklidov algoritam koristi svojstvo da je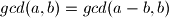 (Tvrdnja 1).
(Tvrdnja 1).
Iz ove tvrdnje jasno vrijedi i da je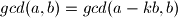 ,
, 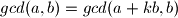 za bilo koji cijeli broj
za bilo koji cijeli broj 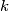
Sam algoritam izgleda ovako:
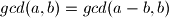 ako
ako 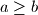
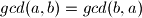 ako
ako 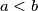
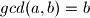 ako
ako 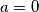
Tako na primjer imamo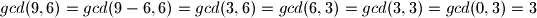
O funkciji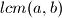 se nema sto pametno reci osim jednakosti break
se nema sto pametno reci osim jednakosti break 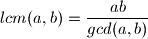 (Tvrdnja 2)
(Tvrdnja 2)
Dokaz tvrnje 1
Neka je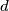 najveci prirodni broj takav da
najveci prirodni broj takav da 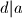 i
i 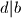 (dakle,
(dakle, 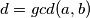 ).
).
Ocito je da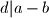 tako da
tako da 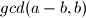 je barem
je barem 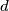 .
.
Pretpostavimo da postoji takav da
takav da 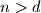 i
i 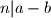 i
i 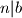 .
.
Tada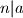 ,
, 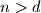 , a
, a 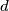 je naveci broj koji djeli i
je naveci broj koji djeli i  i
i  . Kontradikcija, dakle takav
. Kontradikcija, dakle takav  ne postoji.
ne postoji.
Dokaz tvrdnje 2
Zapisimo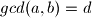
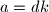
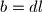 s time da
s time da 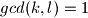 .
.
Znamo da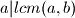 to jest
to jest 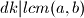 i
i 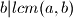 to jest
to jest 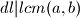 .
.
Kako je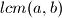 najmanji zajednicki visekratnik, a znamo da je barem
najmanji zajednicki visekratnik, a znamo da je barem 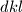 , dobivamo
, dobivamo 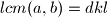 sto se i dobiva uvrstavanjem u formulu
sto se i dobiva uvrstavanjem u formulu 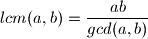
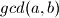 i
i 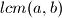 su najcesci zapis za najveceg zajednickog djeljitelja (Greatest Common Divisor) i najmanjeg zajednickog visekratnika (Lowest Common Multiple).
su najcesci zapis za najveceg zajednickog djeljitelja (Greatest Common Divisor) i najmanjeg zajednickog visekratnika (Lowest Common Multiple).Primjetimo prvo da je
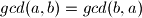 i
i 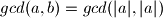 (Jer predznak broja ne mijenja njegove proste djeljitelje)
(Jer predznak broja ne mijenja njegove proste djeljitelje)Funkciju
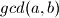 mozemo racunati mnogo brze nego faktorizacijom, pomocu Euklidovog algoritma.
mozemo racunati mnogo brze nego faktorizacijom, pomocu Euklidovog algoritma.Euklidov algoritam koristi svojstvo da je
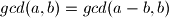 (Tvrdnja 1).
(Tvrdnja 1).Iz ove tvrdnje jasno vrijedi i da je
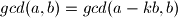 ,
, 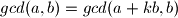 za bilo koji cijeli broj
za bilo koji cijeli broj 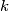
Sam algoritam izgleda ovako:
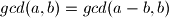 ako
ako 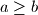
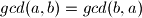 ako
ako 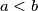
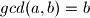 ako
ako 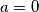
Tako na primjer imamo
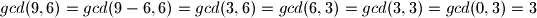
O funkciji
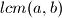 se nema sto pametno reci osim jednakosti break
se nema sto pametno reci osim jednakosti break 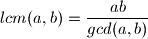 (Tvrdnja 2)
(Tvrdnja 2)Dokaz tvrnje 1
Neka je
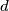 najveci prirodni broj takav da
najveci prirodni broj takav da 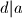 i
i 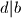 (dakle,
(dakle, 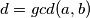 ).
).Ocito je da
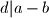 tako da
tako da 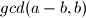 je barem
je barem 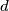 .
.Pretpostavimo da postoji
 takav da
takav da 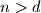 i
i 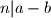 i
i 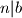 .
.Tada
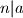 ,
, 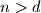 , a
, a 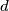 je naveci broj koji djeli i
je naveci broj koji djeli i  i
i  . Kontradikcija, dakle takav
. Kontradikcija, dakle takav  ne postoji.
ne postoji.Dokaz tvrdnje 2
Zapisimo
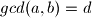
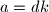
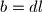 s time da
s time da 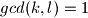 .
.Znamo da
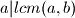 to jest
to jest 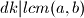 i
i 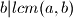 to jest
to jest 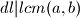 .
.Kako je
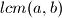 najmanji zajednicki visekratnik, a znamo da je barem
najmanji zajednicki visekratnik, a znamo da je barem 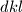 , dobivamo
, dobivamo 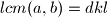 sto se i dobiva uvrstavanjem u formulu
sto se i dobiva uvrstavanjem u formulu 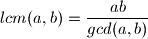
 Školjka
Školjka