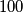Dvadesetoro djece ima vrpci. Svaku vrpcu drže za krajeve dva djeteta. Dva djeteta mogu zajedno držati samo jednu vrpcu. Pretpostavimo da je par vrpci čija četiri kraja drže različita djeca moguće odabrati na 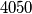načina. Dokaži da svako dijete drži jednak broj vrpci.
Dvadesetoro djece ima $100$ vrpci. Svaku vrpcu drže za krajeve dva djeteta. Dva djeteta mogu zajedno držati samo jednu vrpcu. Pretpostavimo da je par vrpci čija četiri kraja drže različita djeca moguće odabrati na $4050$ načina. Dokaži da svako dijete drži jednak broj vrpci.
Školjka 
vrpci. Svaku vrpcu drže za krajeve dva djeteta. Dva djeteta mogu zajedno držati samo jednu vrpcu. Pretpostavimo da je par vrpci čija četiri kraja drže različita djeca moguće odabrati na 
načina. Dokaži da svako dijete drži jednak broj vrpci.