Dokaži da za sve realne brojeve 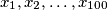 vrijedi nejednakost
vrijedi nejednakost 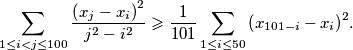
Dokaži da za sve realne brojeve $x_1, x_2, \ldots, x_{100}$ vrijedi nejednakost
\[ \sum_{1 \leq i <j \leq 100} \frac{ {\left(x_j-x_i\right)}^2 }{j^2 - i^2} \geqslant \frac{1}{101} \sum_{1 \leq i \leq 50} {\left(x_{101-i}-x_i\right)}^2.\]