Kliknite ovdje kako biste prikazali rješenje.
Kako bi pojednostavili zapisivanje, uvesti ćemo nekoliko supstitucija. Neka je 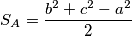 , gdje su
, gdje su  ,
,  i
i  stranice trokuta. Ako je
stranice trokuta. Ako je 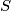 dvostruka površina trokuta
dvostruka površina trokuta 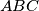 , vrijedi
, vrijedi 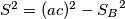 (Tvrdnja slijedi iz činjenice da je
(Tvrdnja slijedi iz činjenice da je 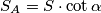 ). Također, iz poznate formule za površinu trokuta slijedi
). Također, iz poznate formule za površinu trokuta slijedi 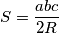 . Iz kosinusovog poučka slijedi da je
. Iz kosinusovog poučka slijedi da je 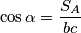 , a iz sinusovog poučka vrijedi
, a iz sinusovog poučka vrijedi 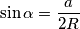 . Sada kada smo "pojednostavili" zapisivanje, možemo početi s rješavanjem.
. Sada kada smo "pojednostavili" zapisivanje, možemo početi s rješavanjem.
Uočimo da prema potenciji točke vrijedi 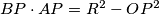 , gdje je
, gdje je 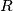 radijus opisane kružnice trokutu
radijus opisane kružnice trokutu 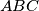 . Primjenom osnovnih trigonometrijskih relacija u trokutima
. Primjenom osnovnih trigonometrijskih relacija u trokutima 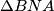 ,
, 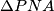 i
i 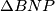 , dobivamo da je
, dobivamo da je 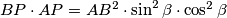 . Analogno, dobivamo da je
. Analogno, dobivamo da je 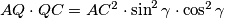 . Kombiniranjem gore danih supstitucija i tvrdnji, dobivamo da je tvrdnja
. Kombiniranjem gore danih supstitucija i tvrdnji, dobivamo da je tvrdnja 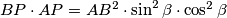 ekvivalentna s tvrdnjom
ekvivalentna s tvrdnjom 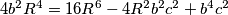 , a da je potrebno dokazati
, a da je potrebno dokazati 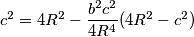 .
.
Preuređivanjem uvjeta dobivamo: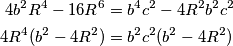 Sada imamo dva slučaja, odnosno, ili je
Sada imamo dva slučaja, odnosno, ili je 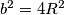 , ili je
, ili je 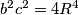 .
.
Ako je 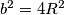 , onda je
, onda je 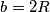 što znači da je trokut pravokutan, a to je u kontradikciji s tvrdnjom da je trokut šiljastokutan.
što znači da je trokut pravokutan, a to je u kontradikciji s tvrdnjom da je trokut šiljastokutan.
Vrijedi da je 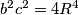 . Ako danu tvrdnju uvrstimo u izraz koji treba dokazati, dobivamo:
. Ako danu tvrdnju uvrstimo u izraz koji treba dokazati, dobivamo: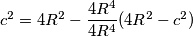 , odnosno,
, odnosno, 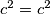 što evidentno vrijedi.
što evidentno vrijedi.
 Školjka
Školjka 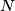 nožište visine iz vrha
nožište visine iz vrha 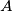 šiljastokutnog trokuta
šiljastokutnog trokuta  i
i 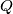 redom nožišta okomica iz točke
redom nožišta okomica iz točke 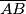 i
i 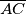 , a točka
, a točka 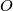 središte opisane kružnice danog trokuta. Ako vrijedi
središte opisane kružnice danog trokuta. Ako vrijedi 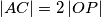 , dokaži da vrijedi
, dokaži da vrijedi 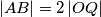 .
.