Točno
2. siječnja 2020. 18:29 (6 godine)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Pretpostavimo suprotno, tj. da su svi  ,
,  i
i  razliciti. Oduzimanjem prve i druge jednakosti dobijemo (nakon faktorizacije):
razliciti. Oduzimanjem prve i druge jednakosti dobijemo (nakon faktorizacije): 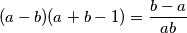 sto zbog pretpostavke mozemo skratiti na
sto zbog pretpostavke mozemo skratiti na 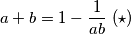 . Analogno dokazemo da vrijede i jednakosti dobivene ciklickom zamjenom varijabli.
. Analogno dokazemo da vrijede i jednakosti dobivene ciklickom zamjenom varijabli.
Ponovno oduzmemo ove prve dvije jednakosti i dobijemo (nakon skracivanja): 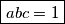 . Iz toga direktno uvrstavanjem u (
. Iz toga direktno uvrstavanjem u ( ) dobijemo
) dobijemo 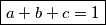 .
.
Sada u pocetnoj jednakosti pise 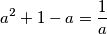 , sto faktoriziramo do jednakosti
, sto faktoriziramo do jednakosti 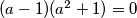 . Iz ovoga citamo jedino realno rjesenje
. Iz ovoga citamo jedino realno rjesenje  . No tada dobijemo sustav
. No tada dobijemo sustav 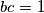
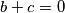 koji nema realnih rjesenja. Zakljucujemo da je pocetna pretpostavka pogresna, tj. neka dva moraju biti jednaka.
koji nema realnih rjesenja. Zakljucujemo da je pocetna pretpostavka pogresna, tj. neka dva moraju biti jednaka.
 Školjka
Školjka 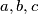 realni brojevi različiti od nule takvi da vrijedi
realni brojevi različiti od nule takvi da vrijedi 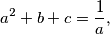
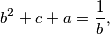
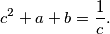 Dokaži da su neka dva od
Dokaži da su neka dva od