Neocijenjeno
20. listopada 2020. 22:13 (5 godine, 3 mjeseci)
Sakrij rješenje
Sakrij rješenje
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Nazovimo skup sa pribrojnicima 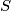 , i skup sa faktorima
, i skup sa faktorima  .
.
Igrajmo se na slučaju 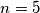 , možda bismo mogli iskoristiti činjenicu da je
, možda bismo mogli iskoristiti činjenicu da je  i podjela na skupove
i podjela na skupove  uistinu radi
uistinu radi
Intuicija nam govori da skup  uopće ne treba toliko puno elemenata, pa pokušajmo pokriti skup
uopće ne treba toliko puno elemenata, pa pokušajmo pokriti skup  sa elementima
sa elementima  i
i  koje ćemo sada otkriti. Dakle
koje ćemo sada otkriti. Dakle 

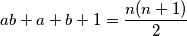
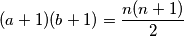
Sada možemo odabrati 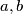 u ovisnosti o parnosti broja
u ovisnosti o parnosti broja  . Ukoliko je
. Ukoliko je  paran odaberimo
paran odaberimo 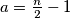 i
i 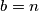 . A ukoliko je
. A ukoliko je  neparan odaberimo
neparan odaberimo 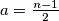 i
i  . Ova konstrukcija očito zadovoljava uvjete zadatka za sve
. Ova konstrukcija očito zadovoljava uvjete zadatka za sve  , čime smo pokazali da se svaki skup
, čime smo pokazali da se svaki skup 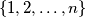 može pocepati na traženi način.
može pocepati na traženi način.
 Školjka
Školjka 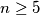 , brojevi
, brojevi 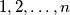 mogu raspodijeliti u dvije grupe takve da je suma elemenata u jednoj grupi jednaka umnošku elemenata druge grupe.
mogu raspodijeliti u dvije grupe takve da je suma elemenata u jednoj grupi jednaka umnošku elemenata druge grupe.