Neocijenjeno
25. listopada 2020. 19:15 (5 godine, 3 mjeseci)
Sakrij rješenje
Sakrij rješenje
Korisnik: MNM
Zadatak: 3. lakša simulacija državnog natjecanja 2020. zadatak 4 (Sakrij tekst zadatka)
Zadatak: 3. lakša simulacija državnog natjecanja 2020. zadatak 4 (Sakrij tekst zadatka)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Pretpostavimo da pravac 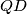 siječe
siječe 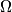 u
u 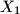 .
.
Primijetimo da je 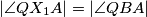 jer su oba obodni kutevi nad lukom
jer su oba obodni kutevi nad lukom 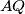 .
.
Uz to, budući da je 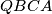 tetivan četverokut i
tetivan četverokut i 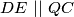 , zaključujemo
, zaključujemo 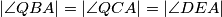 iz čega slijedi
iz čega slijedi 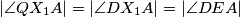 pa je
pa je 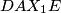 tetivan četverokut.
tetivan četverokut.
Analogno definirajmo 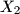 kao presjek pravca
kao presjek pravca 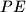 i
i 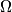 . Sličnim koracima zaključujemo da je
. Sličnim koracima zaključujemo da je 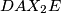 tetivan četverokut.
tetivan četverokut.
Presjek kružnica 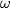 i
i 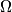 jest još samo jedna točka osim
jest još samo jedna točka osim 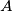 , pa
, pa 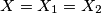 čime je dokaz dovršen.
čime je dokaz dovršen.
 Školjka
Školjka 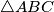 s opisanom kružnicom
s opisanom kružnicom 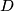 i
i 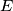 točke na stranicama
točke na stranicama 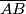 i
i 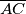 redom takve da vrijedi
redom takve da vrijedi 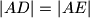 . Neka pravci paralelni s
. Neka pravci paralelni s 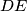 kroz
kroz 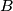 i
i 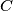 sijeku
sijeku  i
i 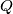 . Neka je
. Neka je 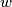 kružnica opisana
kružnica opisana 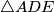 . Dokaži da se pravci
. Dokaži da se pravci