Neocijenjeno
30. prosinca 2022. 16:18 (3 godine, 1 mjesec)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Pretpodstavimo suprotno : Postoje dva broja 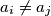 u našim brojevima za koje tvrdnja zadatka vrijedi.
u našim brojevima za koje tvrdnja zadatka vrijedi.
Raspišimo : 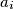
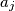
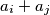
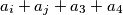
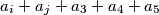

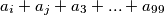
Ovdje ima 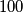 brojeva tako da nikoji nije djeljiv sa
brojeva tako da nikoji nije djeljiv sa 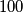 (prema pretpostavci da uvijet zadatka vrijedi ). Prema diriklerovom principu dva imaju isti ostatak (mod 100).
(prema pretpostavci da uvijet zadatka vrijedi ). Prema diriklerovom principu dva imaju isti ostatak (mod 100).
Znamo da 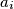 i
i 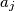 nemaju isti ostatak jer nisu jednaki i manji su od
nemaju isti ostatak jer nisu jednaki i manji su od 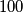 Tako da su neka druga dva i onda kad oduzmemo onaj s manje članova od onog s više članova dobit ćemo da neki izraz :
Tako da su neka druga dva i onda kad oduzmemo onaj s manje članova od onog s više članova dobit ćemo da neki izraz : 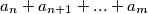 Je djeljiv sa
Je djeljiv sa 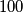
Što je kontradikcija. Prema tome nikoja dva broja nesmiju biti drugačija. Tjst. Svi su brojevi jednaki. Ali također taj broj mora biti relativno prost sa 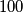 Jer kad bi npr
Jer kad bi npr 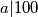
Onda bi 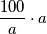 bilo djeljivo sa
bilo djeljivo sa 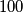
 Školjka
Školjka 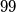 (ne nužno različitih) prirodnih brojeva manjih od
(ne nužno različitih) prirodnih brojeva manjih od