Točno
9. prosinca 2023. 17:47 (2 godine, 1 mjesec)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Ocjene: (1)
Komentari:
ToplaCokolada, 9. prosinca 2023. 17:37
 Školjka
Školjka 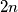 kartica
kartica 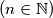 , po dvije kartice sa svakim od brojeva
, po dvije kartice sa svakim od brojeva 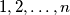 . Kada ih je promiješao i složio jednu do druge u niz, primijetio je da se za svaki
. Kada ih je promiješao i složio jednu do druge u niz, primijetio je da se za svaki 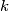 iz skupa
iz skupa 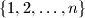 između dvije kartica s brojem
između dvije kartica s brojem 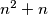 djeljiv s
djeljiv s 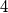 .
. 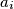 prvi indeks gdje se
prvi indeks gdje se 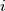 pojavljuje. Onda je
pojavljuje. Onda je 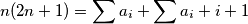
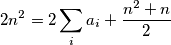 Iz ovoga
Iz ovoga