Točno
25. listopada 2023. 08:02 (2 godine, 3 mjeseci)
Korisnik: prv123
Zadatak: Školsko/gradsko natjecanje iz matematike 2018, SŠ2 A 3 (Sakrij tekst zadatka)
Zadatak: Školsko/gradsko natjecanje iz matematike 2018, SŠ2 A 3 (Sakrij tekst zadatka)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Ocjene: (1)
Komentari:
Patrlk, 25. listopada 2023. 07:27
 Školjka
Školjka 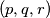 za koje vrijedi
za koje vrijedi 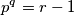
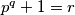
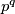 neparan, onda je
neparan, onda je  paran, što je nemoguće, dakle
paran, što je nemoguće, dakle 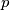 mora biti
mora biti 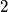 .
.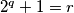
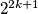 daje
daje 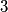 , a
, a 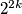 daje
daje 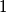 mod 3.
mod 3.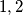 mod
mod 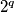 djeljivo s
djeljivo s 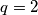 .
. 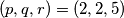
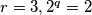 odnosno
odnosno 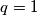 , sto nije prost broj.
, sto nije prost broj. 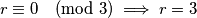 Ovaj slućaj bi bilo barem važno spomenut da nema rješenja.
Ovaj slućaj bi bilo barem važno spomenut da nema rješenja.