Točno
29. listopada 2013. 16:26 (12 godine, 3 mjeseci)
Sakrij rješenje
Sakrij rješenje
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Promatrajmo parnost broja crnih polja. Na pocetku ih je parno ukupno. Neka ih je u retku ili stupcu kojeg zelimo promjeniti prije promjene  . Nakon promjene je u tom retku ili stupcu
. Nakon promjene je u tom retku ili stupcu  . Kako su brojevi
. Kako su brojevi  i
i  iste parnosti, a ostatak tablice nismo mijenjali, znamo da se parnost ukupnog broja crnih polja nije promjenila. Dakle, parnost je konstantna. Kako je na pocetku broj crnih polja paran, a na kraju neparan, jasno je da je to nemoguce postici.
iste parnosti, a ostatak tablice nismo mijenjali, znamo da se parnost ukupnog broja crnih polja nije promjenila. Dakle, parnost je konstantna. Kako je na pocetku broj crnih polja paran, a na kraju neparan, jasno je da je to nemoguce postici.
 . Nakon promjene je u tom retku ili stupcu
. Nakon promjene je u tom retku ili stupcu  . Kako su brojevi
. Kako su brojevi  i
i  iste parnosti, a ostatak tablice nismo mijenjali, znamo da se parnost ukupnog broja crnih polja nije promjenila. Dakle, parnost je konstantna. Kako je na pocetku broj crnih polja paran, a na kraju neparan, jasno je da je to nemoguce postici.
iste parnosti, a ostatak tablice nismo mijenjali, znamo da se parnost ukupnog broja crnih polja nije promjenila. Dakle, parnost je konstantna. Kako je na pocetku broj crnih polja paran, a na kraju neparan, jasno je da je to nemoguce postici.  Školjka
Školjka 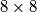 šahovnica obojana je crno bijelo na uobičajen način. U svakom koraku možemo promijeniti boju svih polja u jednom stupcu ili u jednom retku. Možemo li doći do pozicije u kojoj je samo jedno polje crno?
šahovnica obojana je crno bijelo na uobičajen način. U svakom koraku možemo promijeniti boju svih polja u jednom stupcu ili u jednom retku. Možemo li doći do pozicije u kojoj je samo jedno polje crno?