Točno
13. studenoga 2013. 20:31 (12 godine, 2 mjeseci)
Sakrij rješenje
Sakrij rješenje
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Znamo da kvadrati imati samo 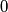 ,
,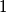 ,
,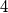 ,
,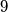 ,
, ili
ili 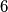 kao zadnju znamenku. Ocitno je
kao zadnju znamenku. Ocitno je 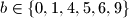 .
.
Znamo i da je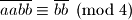
Pogledajmo koje ostatke daju kvadrati pri djeljenju s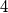 .
.
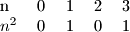
Provjerimo mogucnosti:
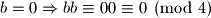 Dakle,
Dakle, 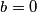 je mogucnost.
je mogucnost.
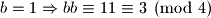 Dakle,
Dakle, 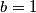 nije mogucnost.
nije mogucnost.
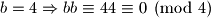 Dakle,
Dakle,  je mogucnost.
je mogucnost.
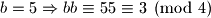 Dakle,
Dakle, 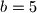 nije mogucnost.
nije mogucnost.
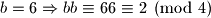 Dakle,
Dakle, 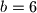 nije mogucnost.
nije mogucnost.
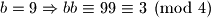 Dakle,
Dakle, 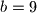 je mogucnost.
je mogucnost.
Sada imamo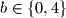
Da bi kvadrat zavrsavo na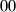 , broj kojeg kvadriramo mora biti djeljiv s
, broj kojeg kvadriramo mora biti djeljiv s 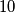 . Brojevi djeljivi s
. Brojevi djeljivi s 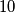 ciji su kvadrati cetveroznamenkasti su
ciji su kvadrati cetveroznamenkasti su 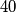 ,
,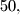 60
60 70
70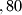 i
i 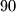 . Niti jedan od njih nedaje kvadrat oblika
. Niti jedan od njih nedaje kvadrat oblika 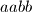 .newline
.newline
 .newline
.newline
Pogledajmo koje ostatke daju kvadrati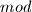
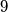 .
.
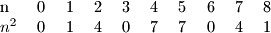
Suma znamenaka naseg broja je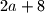
Ispitivanjem modula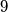 , dobivamo da je
, dobivamo da je 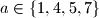 .
.
Iz pravila o djeljivosti s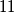 se jasno vidi da je
se jasno vidi da je 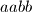 djeljiv s
djeljiv s 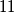 neovisno o vrjednostima
neovisno o vrjednostima  i
i  , tako da za svaki od brojeva provjerimo dali je djeljiv s
, tako da za svaki od brojeva provjerimo dali je djeljiv s 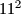 i dobivamo da to zadovoljava samo
i dobivamo da to zadovoljava samo 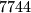 , koji i zaista je kvadrat (
, koji i zaista je kvadrat (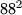 ) .
) .
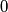 ,
,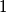 ,
,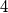 ,
,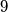 ,
, ili
ili 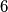 kao zadnju znamenku. Ocitno je
kao zadnju znamenku. Ocitno je 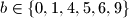 .
.Znamo i da je
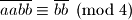
Pogledajmo koje ostatke daju kvadrati pri djeljenju s
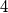 .
.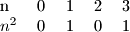
Provjerimo mogucnosti:
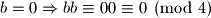 Dakle,
Dakle, 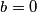 je mogucnost.
je mogucnost.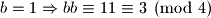 Dakle,
Dakle, 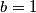 nije mogucnost.
nije mogucnost.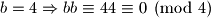 Dakle,
Dakle,  je mogucnost.
je mogucnost.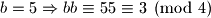 Dakle,
Dakle, 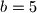 nije mogucnost.
nije mogucnost.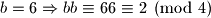 Dakle,
Dakle, 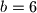 nije mogucnost.
nije mogucnost.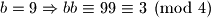 Dakle,
Dakle, 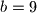 je mogucnost.
je mogucnost.Sada imamo
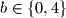
Da bi kvadrat zavrsavo na
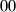 , broj kojeg kvadriramo mora biti djeljiv s
, broj kojeg kvadriramo mora biti djeljiv s 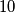 . Brojevi djeljivi s
. Brojevi djeljivi s 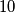 ciji su kvadrati cetveroznamenkasti su
ciji su kvadrati cetveroznamenkasti su 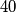 ,
,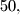 60
60 70
70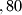 i
i 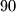 . Niti jedan od njih nedaje kvadrat oblika
. Niti jedan od njih nedaje kvadrat oblika 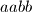 .newline
.newline .newline
.newlinePogledajmo koje ostatke daju kvadrati
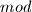
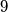 .
.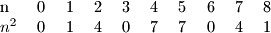
Suma znamenaka naseg broja je
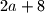
Ispitivanjem modula
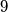 , dobivamo da je
, dobivamo da je 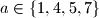 .
.Iz pravila o djeljivosti s
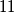 se jasno vidi da je
se jasno vidi da je 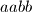 djeljiv s
djeljiv s 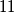 neovisno o vrjednostima
neovisno o vrjednostima  i
i  , tako da za svaki od brojeva provjerimo dali je djeljiv s
, tako da za svaki od brojeva provjerimo dali je djeljiv s 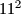 i dobivamo da to zadovoljava samo
i dobivamo da to zadovoljava samo 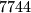 , koji i zaista je kvadrat (
, koji i zaista je kvadrat (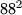 ) .
) .  Školjka
Školjka