Kažemo da je  dobar ako vrijedi
dobar ako vrijedi 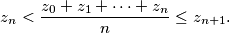 Definiramo
Definiramo 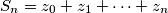 . Dakle, vrijedi
. Dakle, vrijedi 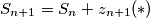 . Uvijet postaje
. Uvijet postaje 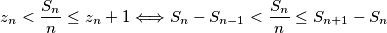 Pomnožimo sve dijelove nejednakosti s
Pomnožimo sve dijelove nejednakosti s  , pa dobivamo
, pa dobivamo 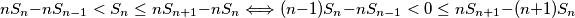 Prisjetimo se
Prisjetimo se 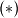 , dobivamo
, dobivamo 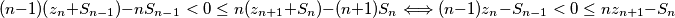 Napravit ćemo jednu kratku opservaciju:
Napravit ćemo jednu kratku opservaciju:
Neka je 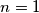 , tada je očito
, tada je očito 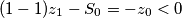 . S druge strane, ako je
. S druge strane, ako je 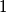 dobar, tada bi vrijedilo
dobar, tada bi vrijedilo 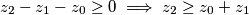 . Tada za sve
. Tada za sve  imamo
imamo 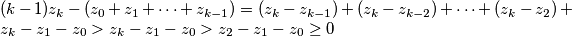
Dakle, nijedan  nije dobar. Tu smo provjerili što se dešava ako je
nije dobar. Tu smo provjerili što se dešava ako je 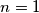 dobar, pa ćemo u ostatku rješenja protpostaviti
dobar, pa ćemo u ostatku rješenja protpostaviti 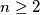 (biti će korisno jer je
(biti će korisno jer je 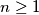 , pa će biti potrebno u nastavku).
, pa će biti potrebno u nastavku).
Sada, neka je 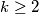 prvi (najmanji) indeks za koji je
prvi (najmanji) indeks za koji je 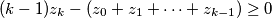 . Znamo da postoji jer je to ekvivalentno tome da je
. Znamo da postoji jer je to ekvivalentno tome da je 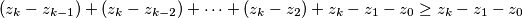 . Kako je za svaki niz
. Kako je za svaki niz 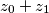 fiksan, a niz je rastući pa
fiksan, a niz je rastući pa 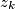 može biti proizvoljno velik, odnosno
može biti proizvoljno velik, odnosno 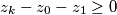 slijedi da takav
slijedi da takav 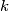 postoji. Za takav
postoji. Za takav 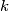 , kako je
, kako je 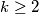 , slijedi da za sve
, slijedi da za sve 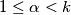 vrijedi
vrijedi 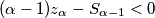 , posebno za
, posebno za 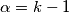 imamo
imamo 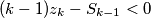 , dakle
, dakle 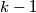 je dobar. Dokažimo da je
je dobar. Dokažimo da je 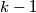 jedini dobar.
jedini dobar.
Primijetimo da nijedan 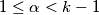 nije dobar, jer vrijedi
nije dobar, jer vrijedi 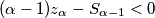 , pa drugi dio nejednakosti nije zadovoljen za sve
, pa drugi dio nejednakosti nije zadovoljen za sve 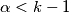 . S druge strane, za sve
. S druge strane, za sve 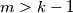 imamo
imamo 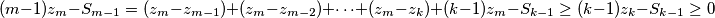 Iz ovoga slijedi da prvi dio nejednakosti nikada nije zadovoljen za sve
Iz ovoga slijedi da prvi dio nejednakosti nikada nije zadovoljen za sve 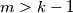 .
.
Iz svega ovoga slijedi da postoji samo jedan dobar broj  .
.
Kažemo da je $n$ dobar ako vrijedi
$$z_n < \frac{z_0 + z_1 + \cdots + z_n}{n} \leq z_{n+1} \text{.}$$
Definiramo $S_n=z_0+z_1+\cdots+z_n$. Dakle, vrijedi $S_{n+1}=S_n+z_{n+1} (*)$. Uvijet postaje
$$z_n<\frac{S_n}{n}\le z_n+1\Longleftrightarrow S_n-S_{n-1}<\frac{S_n}{n}\le S_{n+1}-S_{n}$$
Pomnožimo sve dijelove nejednakosti s $n$, pa dobivamo
$$nS_n-nS_{n-1}<S_n\le nS_{n+1}-nS_n\Longleftrightarrow(n-1)S_n-nS_{n-1}<0\le nS_{n+1}-(n+1)S_n$$
Prisjetimo se $(*)$, dobivamo
$$(n-1)(z_n+S_{n-1})-nS_{n-1}<0\le n(z_{n+1}+S_n)-(n+1)S_n\Longleftrightarrow(n-1)z_n-S_{n-1}<0\le nz_{n+1}-S_n$$
Napravit ćemo jednu kratku opservaciju:\\
Neka je $n=1$, tada je očito $(1-1)z_1-S_0=-z_0<0$. S druge strane, ako je $1$ dobar, tada bi vrijedilo $z_2-z_1-z_0\ge0\implies z_2\ge z_0+z_1$. Tada za sve $k>1$ imamo $(k-1)z_k-(z_0+z_1+\cdots+z_{k-1})=(z_k-z_{k-1})+(z_k-z_{k-2})+\cdots+(z_k-z_2)+z_k-z_1-z_0>z_k-z_1-z_0>z_2-z_1-z_0\ge0$\\
Dakle, nijedan $k>1$ nije dobar. Tu smo provjerili što se dešava ako je $n=1$ dobar, pa ćemo u ostatku rješenja protpostaviti $n\ge2$ (biti će korisno jer je $n\ge1$, pa će biti potrebno u nastavku).
Sada, neka je $k\ge2$ prvi (najmanji) indeks za koji je $(k-1)z_k-(z_0+z_1+\cdots+z_{k-1})\ge0$. Znamo da postoji jer je to ekvivalentno tome da je $(z_k-z_{k-1})+(z_k-z_{k-2})+\cdots+(z_k-z_2)+z_k-z_1-z_0\ge z_k-z_1-z_0$. Kako je za svaki niz $z_0+z_1$ fiksan, a niz je rastući pa $z_k$ može biti proizvoljno velik, odnosno $z_k-z_0-z_1\ge0$ slijedi da takav $k$ postoji. Za takav $k$, kako je $k\ge2$, slijedi da za sve $1\le\alpha<k$ vrijedi $(\alpha-1)z_{\alpha}-S_{\alpha-1}<0$, posebno za $\alpha=k-1$ imamo $(k-1)z_k-S_{k-1}<0$, dakle $k-1$ je dobar. Dokažimo da je $k-1$ jedini dobar.
Primijetimo da nijedan $1\le\alpha<k-1$ nije dobar, jer vrijedi $(\alpha-1)z_{\alpha}-S_{\alpha-1}<0$, pa drugi dio nejednakosti nije zadovoljen za sve $\alpha<k-1$. S druge strane, za sve $m>k-1$ imamo
$$(m-1)z_m-S_{m-1}=(z_m-z_{m-1})+(z_m-z_{m-2})+\cdots+(z_m-z_{k})+(k-1)z_m-S_{k-1}\ge(k-1)z_k-S_{k-1}\ge0$$
Iz ovoga slijedi da prvi dio nejednakosti nikada nije zadovoljen za sve $m>k-1$.\\
Iz svega ovoga slijedi da postoji samo jedan dobar broj $n$.
 dobar ako vrijedi
dobar ako vrijedi 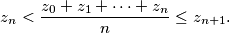 Definiramo
Definiramo 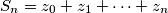 . Dakle, vrijedi
. Dakle, vrijedi 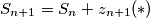 . Uvijet postaje
. Uvijet postaje 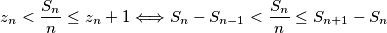 Pomnožimo sve dijelove nejednakosti s
Pomnožimo sve dijelove nejednakosti s  , pa dobivamo
, pa dobivamo 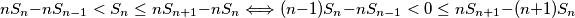 Prisjetimo se
Prisjetimo se 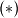 , dobivamo
, dobivamo 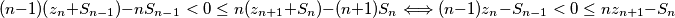 Napravit ćemo jednu kratku opservaciju:
Napravit ćemo jednu kratku opservaciju: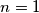 , tada je očito
, tada je očito 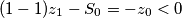 . S druge strane, ako je
. S druge strane, ako je 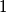 dobar, tada bi vrijedilo
dobar, tada bi vrijedilo 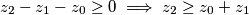 . Tada za sve
. Tada za sve  imamo
imamo 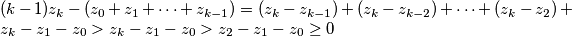
 nije dobar. Tu smo provjerili što se dešava ako je
nije dobar. Tu smo provjerili što se dešava ako je 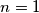 dobar, pa ćemo u ostatku rješenja protpostaviti
dobar, pa ćemo u ostatku rješenja protpostaviti 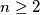 (biti će korisno jer je
(biti će korisno jer je 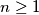 , pa će biti potrebno u nastavku).
, pa će biti potrebno u nastavku).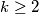 prvi (najmanji) indeks za koji je
prvi (najmanji) indeks za koji je 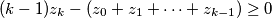 . Znamo da postoji jer je to ekvivalentno tome da je
. Znamo da postoji jer je to ekvivalentno tome da je 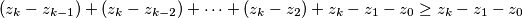 . Kako je za svaki niz
. Kako je za svaki niz 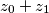 fiksan, a niz je rastući pa
fiksan, a niz je rastući pa 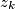 može biti proizvoljno velik, odnosno
može biti proizvoljno velik, odnosno 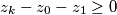 slijedi da takav
slijedi da takav 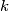 postoji. Za takav
postoji. Za takav 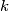 , kako je
, kako je 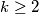 , slijedi da za sve
, slijedi da za sve 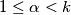 vrijedi
vrijedi 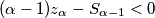 , posebno za
, posebno za 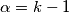 imamo
imamo 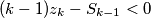 , dakle
, dakle 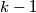 je dobar. Dokažimo da je
je dobar. Dokažimo da je 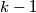 jedini dobar.
jedini dobar.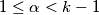 nije dobar, jer vrijedi
nije dobar, jer vrijedi 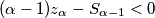 , pa drugi dio nejednakosti nije zadovoljen za sve
, pa drugi dio nejednakosti nije zadovoljen za sve 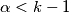 . S druge strane, za sve
. S druge strane, za sve 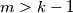 imamo
imamo 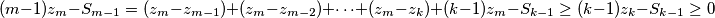 Iz ovoga slijedi da prvi dio nejednakosti nikada nije zadovoljen za sve
Iz ovoga slijedi da prvi dio nejednakosti nikada nije zadovoljen za sve 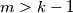 .
. .
.  Školjka
Školjka 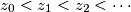 be an infinite sequence of positive integers. Prove that there exists a unique integer
be an infinite sequence of positive integers. Prove that there exists a unique integer 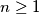 such that
such that