Neocijenjeno
May 5, 2025, 3:28 p.m. (1 year, 3 months)
Let
,
,
be positive real numbers such that
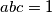
. Prove that
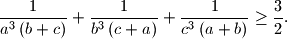
%V0
Let $a$, $b$, $c$ be positive real numbers such that $abc = 1$. Prove that $$\frac {1}{a^{3}\left(b + c\right)} + \frac {1}{b^{3}\left(c + a\right)} + \frac {1}{c^{3}\left(a + b\right)}\geq \frac {3}{2}.$$
Warning: You haven't solved this problem yet.
Click here to display the solution.
Primijetimo da je
$$\frac {1}{a^{3}\left(b + c\right)} + \frac {1}{b^{3}\left(c + a\right)} + \frac {1}{c^{3}\left(a + b\right)}=\frac {a^2b^2c^2}{a^{3}\left(b + c\right)} + \frac {a^2b^2c^2}{b^{3}\left(c + a\right)} + \frac {a^2b^2c^2}{c^{3}\left(a + b\right)}=\frac {b^2c^2}{a\left(b + c\right)} + \frac {c^2a^2}{b\left(c + a\right)} + \frac {a^2b^2}{c\left(a + b\right)}$$
Korištenjem $CSB$ nejednakosti dobivamo
$$\left(a(b+c)+b(c+a)+c(a+b)\right)\left(\frac {b^2c^2}{a\left(b + c\right)} + \frac {c^2a^2}{b\left(c + a\right)} + \frac {a^2b^2}{c\left(a + b\right)}\right)\ge(ab+bc+ca)^2$$
$$\implies \frac {b^2c^2}{a\left(b + c\right)} + \frac {c^2a^2}{b\left(c + a\right)} + \frac {a^2b^2}{c\left(a + b\right)}\ge \frac{(ab+bc+ca)^2}{2(ab+bc+ca)}=\frac{ab+bc+ca}{2}\stackrel{AG}{\ge}\frac{3\sqrt[3]{a^2b^2c^2}}{2}=\frac{3}{2}$$
Što je i trebalo dokazati.
Školjka 
Korištenjem 
nejednakosti dobivamo 
![\implies \frac {b^2c^2}{a\left(b + c\right)} + \frac {c^2a^2}{b\left(c + a\right)} + \frac {a^2b^2}{c\left(a + b\right)}\ge \frac{(ab+bc+ca)^2}{2(ab+bc+ca)}=\frac{ab+bc+ca}{2}\stackrel{AG}{\ge}\frac{3\sqrt[3]{a^2b^2c^2}}{2}=\frac{3}{2}](/media/m/5/7/4/574b66c5e500ca7878a914577ce33a7b.png)
Što je i trebalo dokazati.