Točno
16. svibnja 2025. 11:27 (8 mjeseci, 2 tjedna)
Let $a, b, c$ be positive real numbers such that $abc = 1$. Prove that
$$\frac{a^2-b^2}{a+bc} + \frac{b^2-c^2}{b+ca} + \frac{c^2-a^2}{c+ab} \leq a+b+c-3$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
proširimo li prvi razlomak s  , drugi s
, drugi s  , a treći s
, a treći s  , uvrstimo izraz
, uvrstimo izraz 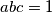 te primjenimo li A-G dobijemo:
te primjenimo li A-G dobijemo:
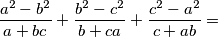
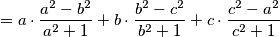
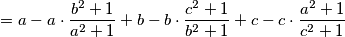
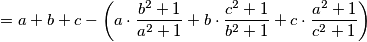
![\overset{\text{A-G}}{\leq} a + b + c - 3 \sqrt[3]{abc}](/media/m/9/7/1/9719eb0560cd5217221b22fa8f64091e.png)
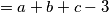 što je i trebalo dokazati.
što je i trebalo dokazati.
proširimo li prvi razlomak s \(a\), drugi s \(b\), a treći s \(c\), uvrstimo izraz \(abc=1\) te primjenimo li A-G dobijemo:
\[
\frac{a^2 - b^2}{a + bc} + \frac{b^2 - c^2}{b + ca} + \frac{c^2 - a^2}{c + ab} =
\]
\[
= a \cdot \frac{a^2 - b^2}{a^2 + 1} + b \cdot \frac{b^2 - c^2}{b^2 + 1} + c \cdot \frac{c^2 - a^2}{c^2 + 1}
\]
\[
= a - a \cdot \frac{b^2 + 1}{a^2 + 1} + b - b \cdot \frac{c^2 + 1}{b^2 + 1} + c - c \cdot \frac{a^2 + 1}{c^2 + 1}
\]
\[
= a + b + c - \left( a \cdot \frac{b^2 + 1}{a^2 + 1} + b \cdot \frac{c^2 + 1}{b^2 + 1} + c \cdot \frac{a^2 + 1}{c^2 + 1} \right)
\]
\[
\overset{\text{A-G}}{\leq} a + b + c - 3 \sqrt[3]{abc}
\]
\[
= a + b + c - 3
\]
što je i trebalo dokazati.
| 8. srpnja 2025. 20:19 | Patrlk | Točno |