Točno
29. svibnja 2015. 00:58 (10 godine, 8 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
n(n+1)(n+2)(n+3) je uvijek djeljivo sa 4 jer u svaka 4 uzastopna broja postoje točno 2 koja su djeljiva sa 2, a prema tome im je umnožak djeljiv sa 4.
m? je umnožak prvih m prostih brojeva, od kojih je samo 2 paran, pa je m? djeljiv sa 2 samo jednom te nikad nije djeljiv sa 4.
Prema tome, m? nikako ne može biti jednako n(n+1)(n+2)(n+3).
m? je umnožak prvih m prostih brojeva, od kojih je samo 2 paran, pa je m? djeljiv sa 2 samo jednom te nikad nije djeljiv sa 4.
Prema tome, m? nikako ne može biti jednako n(n+1)(n+2)(n+3).
 Školjka
Školjka  neka je
neka je 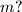 umnožak prvih
umnožak prvih  takvi da je
takvi da je 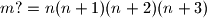 .
.