Točno
5. lipnja 2015. 14:44 (10 godine, 8 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
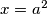

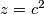
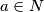
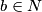
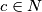
Pa tako vrijede jednadžbe

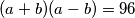
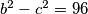

96 je umnožak
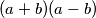 i umnožak
i umnožak 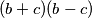 i djeljiv je s brojevima 1,2,3,4,6,8,12,16,24,32,48 i 96. pa tako
i djeljiv je s brojevima 1,2,3,4,6,8,12,16,24,32,48 i 96. pa tako 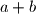 i
i 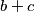 mogu biti brojevi 96,48,32,24,16 i 12 jer
mogu biti brojevi 96,48,32,24,16 i 12 jer  i
i 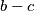 mogu biti brojevi 1,2,3,4,6 i 8
mogu biti brojevi 1,2,3,4,6 i 8Pa tako jer
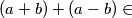 {
{ 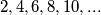 } proizlazi da
} proizlazi da 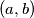 i
i 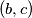 mogu biti samo
mogu biti samo 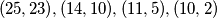 ,a kako u oba uređena para broj
,a kako u oba uređena para broj  mora biti isti što znači da je moguće samo:
mora biti isti što znači da je moguće samo: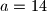


pa postoji i samo uređena trojka
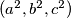 to jest
to jest 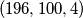 za koju vrijedi
za koju vrijedi 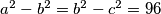
Ocjene: (1)
Komentari:
ikicic, 7. lipnja 2015. 22:12
PatricijaVelecki, 7. lipnja 2015. 12:06
ikicic, 5. lipnja 2015. 21:34
PatricijaVelecki, 5. lipnja 2015. 21:14
Hvala na ispravku rješenja i upozorenju što bih još trebala dopuniti,ali jednostavno nisam znala kako da drugačije napišem da je to tako jer je 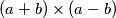 umnožak koji mora biti 96
umnožak koji mora biti 96
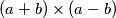 umnožak koji mora biti 96
umnožak koji mora biti 96Cudno malo izgleda formulacija "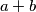 mogu biti brojevi (...), jer
mogu biti brojevi (...), jer 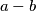 mogu biti (...)".
mogu biti (...)".
U smislu, zasto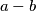 mogu biti tocno ti brojevi?
mogu biti tocno ti brojevi?
No, radi se o finesama samo...
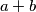 mogu biti brojevi (...), jer
mogu biti brojevi (...), jer 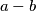 mogu biti (...)".
mogu biti (...)".U smislu, zasto
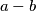 mogu biti tocno ti brojevi?
mogu biti tocno ti brojevi?No, radi se o finesama samo...
Zadnja promjena: PatricijaVelecki, 5. lipnja 2015. 21:14
ikicic, 5. lipnja 2015. 21:04
PatricijaVelecki, 5. lipnja 2015. 19:53
Ja sam mislila da je dovoljno napisati da je 96 djeljiv s 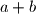 i
i  i s ovim navedenim brojevima,pa da je odmah slijedilo iz toga da je
i s ovim navedenim brojevima,pa da je odmah slijedilo iz toga da je 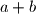 >
>  pa samim time proizlazi i onaj raspored mogućih
pa samim time proizlazi i onaj raspored mogućih 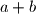 i onda na kraju uređeni parovi
i onda na kraju uređeni parovi
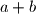 i
i  i s ovim navedenim brojevima,pa da je odmah slijedilo iz toga da je
i s ovim navedenim brojevima,pa da je odmah slijedilo iz toga da je 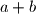 >
>  pa samim time proizlazi i onaj raspored mogućih
pa samim time proizlazi i onaj raspored mogućih 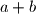 i onda na kraju uređeni parovi
i onda na kraju uređeni paroviNedostaju samo malo konkretniji argumenti. Primjerice, dio s mogucim vrijednostima izraza 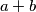 i
i 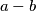 , bilo bi dobro reci otkud takav zakljucak.
, bilo bi dobro reci otkud takav zakljucak.
Mozes reci recimo da to slijedi iz toga sto je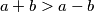 , pa je
, pa je 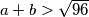 i
i 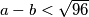 .
.
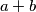 i
i 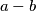 , bilo bi dobro reci otkud takav zakljucak.
, bilo bi dobro reci otkud takav zakljucak.Mozes reci recimo da to slijedi iz toga sto je
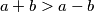 , pa je
, pa je 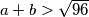 i
i 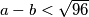 .
.ikicic, 5. lipnja 2015. 19:47
 Školjka
Školjka 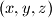 za koje je:
za koje je: 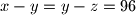 , pri čemu su
, pri čemu su  ,
, 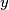 ,
,  kvadrati prirodnih brojeva.
kvadrati prirodnih brojeva. 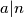 , onda je sigurno barem jedan od brojeva
, onda je sigurno barem jedan od brojeva  i
i 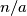 manji ili jednak
manji ili jednak 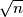 ).
).