Točno
20. prosinca 2015. 22:51 (10 godine, 1 mjesec)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
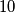 i
i 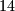 moramo izbaciti jer kad bi oni ostali u skupu, umnožak bi bio djeljiv s
moramo izbaciti jer kad bi oni ostali u skupu, umnožak bi bio djeljiv s  , odnosno
, odnosno 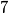 , a nebi bio djeljiv s
, a nebi bio djeljiv s  , odnosno
, odnosno 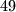 pa ne bi bio potpun kvadrat. Umnožak preostalih brojeva nije potpun kvadrat, jer je najveća potencija broja
pa ne bi bio potpun kvadrat. Umnožak preostalih brojeva nije potpun kvadrat, jer je najveća potencija broja 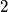 koja ga dijeli neparna, odnosno iznosi
koja ga dijeli neparna, odnosno iznosi 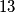 . Ili ga možemo naprosto izračunati, to je broj
. Ili ga možemo naprosto izračunati, to je broj 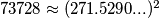 . Odnosno, moramo izbaciti barem
. Odnosno, moramo izbaciti barem 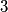 elementa. Sad je jasno ako izbacimo još
elementa. Sad je jasno ako izbacimo još 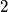 ili
ili 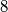 , rezultat će biti potpuni kvadrat. Dakle, na primjer, ako izbacimo
, rezultat će biti potpuni kvadrat. Dakle, na primjer, ako izbacimo 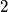 ,
, 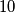 i
i 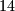 , umnožak preostalih brojeva je
, umnožak preostalih brojeva je 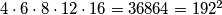 , pa je odgovor
, pa je odgovor 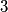 elementa.
elementa.  Školjka
Školjka 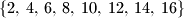 tako da umnožak preostalih elemenata bude kvadrat prirodnog broja?
tako da umnožak preostalih elemenata bude kvadrat prirodnog broja?