Točno
19. siječnja 2016. 22:43 (10 godine)
Korisnik: Daniel_Sirola
Zadatak: Simulacija općinskog 2016. za prvi razred zadatak 5. (Sakrij tekst zadatka)
Zadatak: Simulacija općinskog 2016. za prvi razred zadatak 5. (Sakrij tekst zadatka)
Svaki od  kuhara zna dio nekog recepta za kolač (i svi znaju različite dijelove recepta, a zajedno znaju čitav recept). Dopušteno im je razmjenjivanje svih informacija koje znaju preko telefona, ali tako da u jednom telefonskom razgovoru sudjeluju točno dva kuhara i tijekom tog razgovora točno jedan od njih govori. Odredite najmanji broj telefonskih poziva potrebnih da bi svi kuhari znali čitav recept.
kuhara zna dio nekog recepta za kolač (i svi znaju različite dijelove recepta, a zajedno znaju čitav recept). Dopušteno im je razmjenjivanje svih informacija koje znaju preko telefona, ali tako da u jednom telefonskom razgovoru sudjeluju točno dva kuhara i tijekom tog razgovora točno jedan od njih govori. Odredite najmanji broj telefonskih poziva potrebnih da bi svi kuhari znali čitav recept.
 kuhara zna dio nekog recepta za kolač (i svi znaju različite dijelove recepta, a zajedno znaju čitav recept). Dopušteno im je razmjenjivanje svih informacija koje znaju preko telefona, ali tako da u jednom telefonskom razgovoru sudjeluju točno dva kuhara i tijekom tog razgovora točno jedan od njih govori. Odredite najmanji broj telefonskih poziva potrebnih da bi svi kuhari znali čitav recept.
kuhara zna dio nekog recepta za kolač (i svi znaju različite dijelove recepta, a zajedno znaju čitav recept). Dopušteno im je razmjenjivanje svih informacija koje znaju preko telefona, ali tako da u jednom telefonskom razgovoru sudjeluju točno dva kuhara i tijekom tog razgovora točno jedan od njih govori. Odredite najmanji broj telefonskih poziva potrebnih da bi svi kuhari znali čitav recept. Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Na početku je potrebno zaključiti da će kuhari u konačno mnogo poteza svi saznati recept.
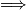 Možemo pretpostaviti da za
Možemo pretpostaviti da za  kuhara postoji raspored s najmanje rezgovora potrebnih da svi znaju sve.
kuhara postoji raspored s najmanje rezgovora potrebnih da svi znaju sve.
Također, bitno je vidjeti da će se svaki kuhar nalaziti u najmanje 2 razgovora (jer mora ostalima reći što on zna, te ostali njemu što oni znaju).
Promatrajmo sada što bi se dogodilo kada bismo dodali još jednog kuhara, odnosno gledali situaciju s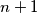 kuharom.
kuharom.
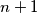 . kuhar također mora obaviti barem 2 razgovora. Dokažimo da je to dovoljno.
. kuhar također mora obaviti barem 2 razgovora. Dokažimo da je to dovoljno.
Slijedeća konstrukcija to pokazuje: taj kuhar poziva bilo kojeg od ostalih i kazuje što zna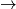 ostalih ima
ostalih ima  i svi zajedno znaju čitav recept, dakle u
i svi zajedno znaju čitav recept, dakle u 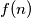 poteza svaki od preostalih
poteza svaki od preostalih  zna recept
zna recept 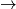 jedan od njih naziva
jedan od njih naziva 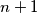 . kuhara i kazuje mu cijeli recept.
. kuhara i kazuje mu cijeli recept.
Dakle
I trivijalno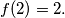
Odavdje jednostavno indukcijom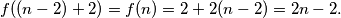
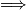 Možemo pretpostaviti da za
Možemo pretpostaviti da za  kuhara postoji raspored s najmanje rezgovora potrebnih da svi znaju sve.
kuhara postoji raspored s najmanje rezgovora potrebnih da svi znaju sve.Također, bitno je vidjeti da će se svaki kuhar nalaziti u najmanje 2 razgovora (jer mora ostalima reći što on zna, te ostali njemu što oni znaju).
Promatrajmo sada što bi se dogodilo kada bismo dodali još jednog kuhara, odnosno gledali situaciju s
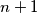 kuharom.
kuharom.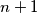 . kuhar također mora obaviti barem 2 razgovora. Dokažimo da je to dovoljno.
. kuhar također mora obaviti barem 2 razgovora. Dokažimo da je to dovoljno.Slijedeća konstrukcija to pokazuje: taj kuhar poziva bilo kojeg od ostalih i kazuje što zna
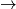 ostalih ima
ostalih ima  i svi zajedno znaju čitav recept, dakle u
i svi zajedno znaju čitav recept, dakle u 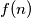 poteza svaki od preostalih
poteza svaki od preostalih  zna recept
zna recept 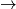 jedan od njih naziva
jedan od njih naziva 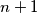 . kuhara i kazuje mu cijeli recept.
. kuhara i kazuje mu cijeli recept.Dakle

I trivijalno
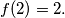
Odavdje jednostavno indukcijom
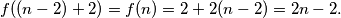
Ocjene: (1)
Komentari:
Daniel_Sirola, 19. siječnja 2016. 22:44
 Školjka
Školjka