Točno
2. travnja 2016. 19:41 (9 godine, 10 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Ako tvrdnja vrijedi tada postoji prirodni broj  takav da
takav da
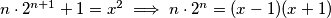
 je neparan, a
je neparan, a  i
i 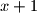 su udaljeni točno za dva pa je jedan djeljiv sa
su udaljeni točno za dva pa je jedan djeljiv sa 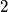 , a drugi sa
, a drugi sa 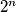 pa razlikujemo dva slučaja:
pa razlikujemo dva slučaja:
1)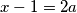 ,
, 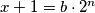 gdje su
gdje su 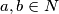 ,
, 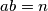
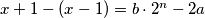
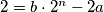
Gledamo minimalnu vrijednost funkcije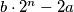
za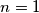 imamo minimalnu vrijednost
imamo minimalnu vrijednost 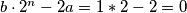
za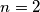 imamo
imamo 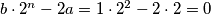
za imamo
imamo 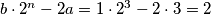
za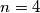 imamo
imamo 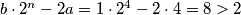
Za veće nemoramo provjeravati jer
nemoramo provjeravati jer 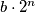 raste eksponencijalno, a
raste eksponencijalno, a 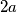 linearno pa se minimalna vrijednost povećava
linearno pa se minimalna vrijednost povećava
Zaključujemo: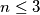
2)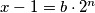 ,
, 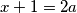 gdje su
gdje su 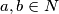 ,
, 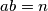
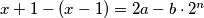
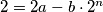
Gledamo maksimalnu vrijednost funkcije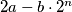
za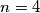 imamo
imamo 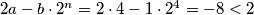
Za veće nemoramo provjeravati jer
nemoramo provjeravati jer 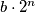 raste eksponencijalno, a
raste eksponencijalno, a 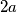 linearno pa se maksimalna vrijednost smanjuje
linearno pa se maksimalna vrijednost smanjuje
Zaključujemo: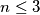
Uvrštavajući sve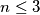 u
u 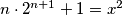 dobijemo da je
dobijemo da je  jedino rješenje.
jedino rješenje.
 takav da
takav da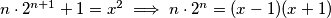
 je neparan, a
je neparan, a  i
i 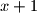 su udaljeni točno za dva pa je jedan djeljiv sa
su udaljeni točno za dva pa je jedan djeljiv sa 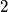 , a drugi sa
, a drugi sa 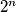 pa razlikujemo dva slučaja:
pa razlikujemo dva slučaja:1)
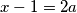 ,
, 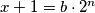 gdje su
gdje su 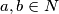 ,
, 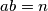
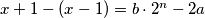
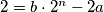
Gledamo minimalnu vrijednost funkcije
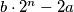
za
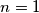 imamo minimalnu vrijednost
imamo minimalnu vrijednost 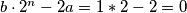
za
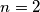 imamo
imamo 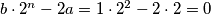
za
 imamo
imamo 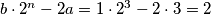
za
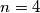 imamo
imamo 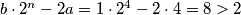
Za veće
 nemoramo provjeravati jer
nemoramo provjeravati jer 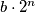 raste eksponencijalno, a
raste eksponencijalno, a 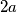 linearno pa se minimalna vrijednost povećava
linearno pa se minimalna vrijednost povećavaZaključujemo:
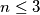
2)
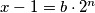 ,
, 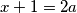 gdje su
gdje su 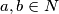 ,
, 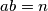
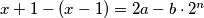
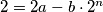
Gledamo maksimalnu vrijednost funkcije
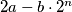
za
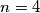 imamo
imamo 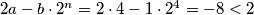
Za veće
 nemoramo provjeravati jer
nemoramo provjeravati jer 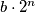 raste eksponencijalno, a
raste eksponencijalno, a 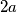 linearno pa se maksimalna vrijednost smanjuje
linearno pa se maksimalna vrijednost smanjujeZaključujemo:
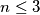
Uvrštavajući sve
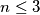 u
u 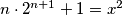 dobijemo da je
dobijemo da je  jedino rješenje.
jedino rješenje. Ocjene: (1)
Komentari:
grga, 18. travnja 2016. 19:31
 Školjka
Školjka 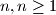 ,such that
,such that 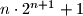 is a perfect square
is a perfect square 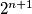
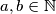 takve da je
takve da je