Točno
19. rujna 2016. 06:40 (9 godine, 4 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Neka je 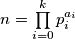 . Nađimo pomoću toga sumu djelitelja
. Nađimo pomoću toga sumu djelitelja  . Neka je to funkcija
. Neka je to funkcija 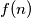 . Tada je
. Tada je 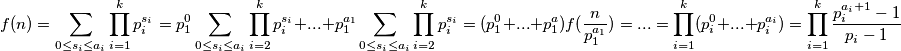 .
.
Iz toga da je 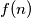 potencija dva slijedi da je
potencija dva slijedi da je 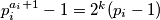 .
.
Radi jasnoće (XD) zapišimo to u općenitijem obliku 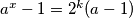 . Neka je
. Neka je 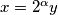 gdje je
gdje je 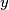 neparan. Tada
neparan. Tada 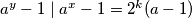 . Slijedi da je
. Slijedi da je 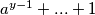 potencija dva, ali kako je
potencija dva, ali kako je 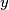 neparan dolazimo do kontradikcije pa je
neparan dolazimo do kontradikcije pa je 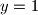 odnosno
odnosno  potencija broja dva.
potencija broja dva.
U našem slučaju je to 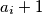 potencija broja dva. Kako je broj djelitelja po poznatoj lemmi
potencija broja dva. Kako je broj djelitelja po poznatoj lemmi 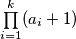 to je onda također potencija broja dva, što je i trebalo dokazati.
to je onda također potencija broja dva, što je i trebalo dokazati.
Ocjene: (1)
Komentari:
rhldj, 19. rujna 2016. 06:41
 Školjka
Školjka  is a power of two, then the number/amount of the divisors is a power of two.
is a power of two, then the number/amount of the divisors is a power of two. 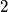 a to nam je bitan dio. Ispravljeno.
a to nam je bitan dio. Ispravljeno. 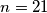 , tvrdnja zadatka je zadovoljena, ali
, tvrdnja zadatka je zadovoljena, ali 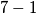 nije potencija broja
nije potencija broja 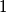 .
.