Let
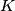
denote the set
.
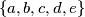
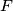
is a collection of
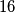
different subsets of
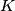
, and it is known that any three members of
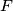
have at least one element in common. Show that all
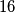
members of
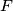
have exactly one element in common.
%V0
Let $K$ denote the set $\{a, b, c, d, e\}$. $F$ is a collection of $16$ different subsets of $K$, and it is known that any three members of $F$ have at least one element in common. Show that all $16$ members of $F$ have exactly one element in common.
Školjka