A circle

with center
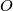
on base
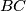
of an isosceles triangle
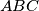
is tangent to the equal sides
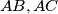
. If point

on

and point
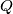
on
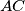
are selected such that
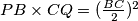
, prove that line segment
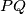
is tangent to circle

, and prove the converse.
%V0
A circle $C$ with center $O$ on base $BC$ of an isosceles triangle $ABC$ is tangent to the equal sides $AB,AC$. If point $P$ on $AB$ and point $Q$ on $AC$ are selected such that $PB \times CQ = (\frac{BC}{2})^2$, prove that line segment $PQ$ is tangent to circle $C$, and prove the converse.