Let
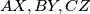
be three cevians concurrent at an interior point
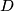
of a triangle
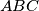
. Prove that if two of the quadrangles
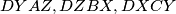
are circumscribable, so is the third.
%V0
Let $AX,BY,CZ$ be three cevians concurrent at an interior point $D$ of a triangle $ABC$. Prove that if two of the quadrangles $DY AZ,DZBX,DXCY$ are circumscribable, so is the third.
Školjka