Does there exist a set
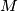
in usual Euclidean space such that for every plane
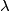
the intersection
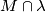
is finite and nonempty ?
Proposed by Hungary.
RemarkI'm not sure I'm posting this in a right Forum.
%V0
Does there exist a set $M$ in usual Euclidean space such that for every plane $\lambda$ the intersection $M \cap \lambda$ is finite and nonempty ?
Proposed by Hungary.
RemarkI'm not sure I'm posting this in a right Forum.
Školjka