Let
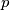
be the product of two consecutive integers greater than 2. Show that there are no integers
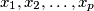
satisfying the equation
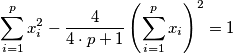
OR
Show that there are only two values of
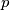
for which there are integers
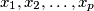
satisfying
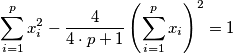
%V0
Let $p$ be the product of two consecutive integers greater than 2. Show that there are no integers $x_1, x_2, \ldots, x_p$ satisfying the equation
$$\sum^p_{i = 1} x^2_i - \frac {4}{4 \cdot p + 1} \left( \sum^p_{i = 1} x_i \right)^2 = 1$$
OR
Show that there are only two values of $p$ for which there are integers $x_1, x_2, \ldots, x_p$ satisfying
$$\sum^p_{i = 1} x^2_i - \frac {4}{4 \cdot p + 1} \left( \sum^p_{i = 1} x_i \right)^2 = 1$$