Show that any two points lying inside a regular
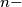
gon
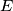
can be joined by two circular arcs lying inside
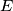
and meeting at an angle of at least
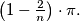
%V0
Show that any two points lying inside a regular $n-$gon $E$ can be joined by two circular arcs lying inside $E$ and meeting at an angle of at least $\left(1 - \frac{2}{n} \right) \cdot \pi.$
Školjka