For each finite set 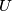 of nonzero vectors in the plane we define
of nonzero vectors in the plane we define 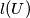 to be the length of the vector that is the sum of all vectors in
to be the length of the vector that is the sum of all vectors in 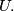 Given a finite set
Given a finite set 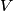 of nonzero vectors in the plane, a subset
of nonzero vectors in the plane, a subset 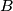 of
of 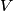 is said to be maximal if
is said to be maximal if 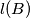 is greater than or equal to
is greater than or equal to 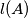 for each nonempty subset
for each nonempty subset  of
of 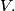
(a) Construct sets of 4 and 5 vectors that have 8 and 10 maximal subsets respectively.
(b) Show that, for any set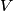 consisting of
consisting of 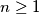 vectors the number of maximal subsets is less than or equal to
vectors the number of maximal subsets is less than or equal to 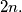
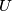 of nonzero vectors in the plane we define
of nonzero vectors in the plane we define 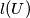 to be the length of the vector that is the sum of all vectors in
to be the length of the vector that is the sum of all vectors in 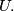 Given a finite set
Given a finite set 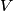 of nonzero vectors in the plane, a subset
of nonzero vectors in the plane, a subset 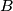 of
of 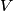 is said to be maximal if
is said to be maximal if 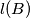 is greater than or equal to
is greater than or equal to 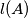 for each nonempty subset
for each nonempty subset  of
of 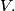
(a) Construct sets of 4 and 5 vectors that have 8 and 10 maximal subsets respectively.
(b) Show that, for any set
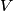 consisting of
consisting of 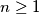 vectors the number of maximal subsets is less than or equal to
vectors the number of maximal subsets is less than or equal to 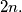
 Školjka
Školjka