Let 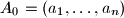 be a finite sequence of real numbers. For each
be a finite sequence of real numbers. For each 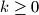 , from the sequence
, from the sequence 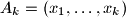 we construct a new sequence
we construct a new sequence 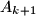 in the following way.
in the following way.
1. We choose a partition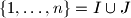 , where
, where  and
and 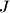 are two disjoint sets, such that the expression
are two disjoint sets, such that the expression
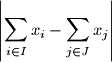
attains the smallest value. (We allow or
or 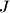 to be empty; in this case the corresponding sum is 0.) If there are several such partitions, one is chosen arbitrarily.
to be empty; in this case the corresponding sum is 0.) If there are several such partitions, one is chosen arbitrarily.
2. We set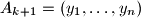 where
where 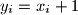 if
if 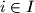 , and
, and 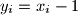 if
if 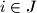 .
.
Prove that for some , the sequence
, the sequence 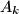 contains an element
contains an element  such that
such that 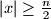 .
.
Author: Omid Hatami, Iran
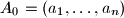 be a finite sequence of real numbers. For each
be a finite sequence of real numbers. For each 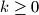 , from the sequence
, from the sequence 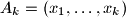 we construct a new sequence
we construct a new sequence 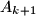 in the following way.
in the following way. 1. We choose a partition
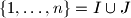 , where
, where  and
and 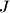 are two disjoint sets, such that the expression
are two disjoint sets, such that the expression 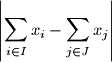
attains the smallest value. (We allow
 or
or 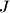 to be empty; in this case the corresponding sum is 0.) If there are several such partitions, one is chosen arbitrarily.
to be empty; in this case the corresponding sum is 0.) If there are several such partitions, one is chosen arbitrarily. 2. We set
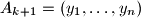 where
where 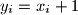 if
if 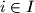 , and
, and 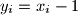 if
if 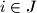 .
. Prove that for some
 , the sequence
, the sequence 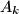 contains an element
contains an element  such that
such that 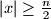 .
. Author: Omid Hatami, Iran
 Školjka
Školjka