IMO Shortlist 2005 problem C3
Kvaliteta:
Avg: 0,0Težina:
Avg: 7,0 Consider a 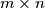 rectangular board consisting of
rectangular board consisting of  unit squares. Two of its unit squares are called adjacent if they have a common edge, and a path is a sequence of unit squares in which any two consecutive squares are adjacent. Two parths are called non-intersecting if they don't share any common squares.
unit squares. Two of its unit squares are called adjacent if they have a common edge, and a path is a sequence of unit squares in which any two consecutive squares are adjacent. Two parths are called non-intersecting if they don't share any common squares.
Each unit square of the rectangular board can be colored black or white. We speak of a coloring of the board if all its unit squares are colored.
unit squares are colored.
Let be the number of colorings of the board such that there exists at least one black path from the left edge of the board to its right edge. Let
be the number of colorings of the board such that there exists at least one black path from the left edge of the board to its right edge. Let  be the number of colorings of the board for which there exist at least two non-intersecting black paths from the left edge of the board to its right edge.
be the number of colorings of the board for which there exist at least two non-intersecting black paths from the left edge of the board to its right edge.
Prove that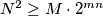 .
.
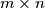 rectangular board consisting of
rectangular board consisting of  unit squares. Two of its unit squares are called adjacent if they have a common edge, and a path is a sequence of unit squares in which any two consecutive squares are adjacent. Two parths are called non-intersecting if they don't share any common squares.
unit squares. Two of its unit squares are called adjacent if they have a common edge, and a path is a sequence of unit squares in which any two consecutive squares are adjacent. Two parths are called non-intersecting if they don't share any common squares. Each unit square of the rectangular board can be colored black or white. We speak of a coloring of the board if all its
 unit squares are colored.
unit squares are colored. Let
 be the number of colorings of the board such that there exists at least one black path from the left edge of the board to its right edge. Let
be the number of colorings of the board such that there exists at least one black path from the left edge of the board to its right edge. Let  be the number of colorings of the board for which there exist at least two non-intersecting black paths from the left edge of the board to its right edge.
be the number of colorings of the board for which there exist at least two non-intersecting black paths from the left edge of the board to its right edge. Prove that
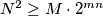 .
. Izvor: Međunarodna matematička olimpijada, shortlist 2005
 Školjka
Školjka 
