Let 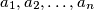 be distinct positive integers and let
be distinct positive integers and let  be a set of
be a set of 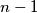 positive integers not containing
positive integers not containing 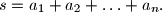 A grasshopper is to jump along the real axis, starting at the point
A grasshopper is to jump along the real axis, starting at the point 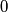 and making
and making  jumps to the right with lengths
jumps to the right with lengths 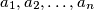 in some order. Prove that the order can be chosen in such a way that the grasshopper never lands on any point in
in some order. Prove that the order can be chosen in such a way that the grasshopper never lands on any point in 
Proposed by Dmitry Khramtsov, Russia
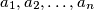 be distinct positive integers and let
be distinct positive integers and let  be a set of
be a set of 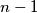 positive integers not containing
positive integers not containing 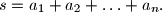 A grasshopper is to jump along the real axis, starting at the point
A grasshopper is to jump along the real axis, starting at the point 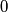 and making
and making  jumps to the right with lengths
jumps to the right with lengths 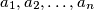 in some order. Prove that the order can be chosen in such a way that the grasshopper never lands on any point in
in some order. Prove that the order can be chosen in such a way that the grasshopper never lands on any point in 
Proposed by Dmitry Khramtsov, Russia
 Školjka
Školjka